Галопирование вагона что это
Виды колебания кузова вагона
Во время движения по рельсовому пути кузов вагона испытывает сложные колебательные движения. Эти колебания возбуждаются динамическими усилиями и обусловливаются неровностями пути, наличием зазоров на стыковых рельсовых соединениях, коничностью поверхности катания колесных пар, а также наличием неровностей на этой поверхности, непостоянством физических свойств материалов пути и колесных пар, типом рессорного подвешивания, изменением скорости вагона и друрими.
Рессорное подвешивание и гасители колебаний, применяемые в вагонах, уменьшают влияние динамических усилий и обеспечивают более плавное движение вагона. Однако действие этих усилий (вертикальных, поперечных и продольных) настолько существенно, что обрессоренные массы вагонов приходят в колебательное состояние.
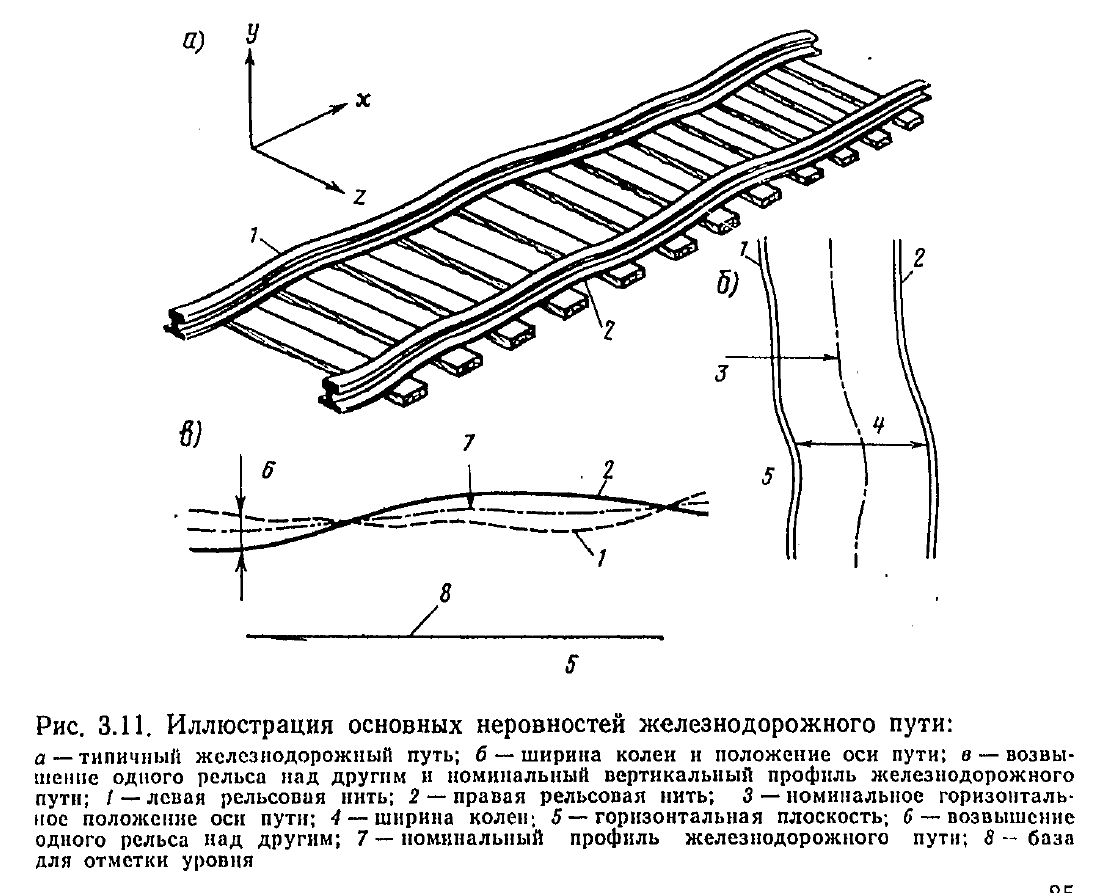
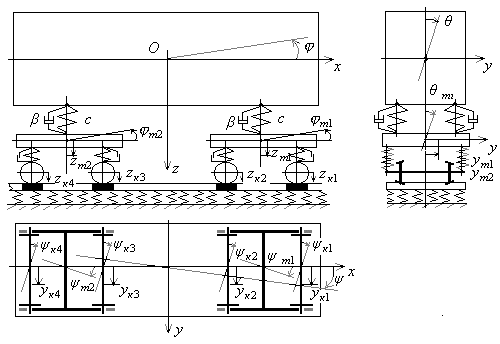
При изучении колебаний кузова вагона он рассматривается в пространственной системе координат (рис. 1, а) как твердое тело. Под влиянием действующих на вагон сил могут возникать следующие виды главных колебаний.
Рис. 1 – Главные виды колебаний
Подпрыгивание, когда обрессоренные части вагона перемещаются вверх и вниз параллельно первоначальному положению по оси z–z на величину ±z (рис. 1, б), возникает под действием вертикальных динамических сил, вызывающих одинаковые ускорения по концам кузова.
Продольная качка или галопирование – обрессоренные части вагона совершают вращательное движение относительно оси у–у на некоторый угол ±θ (рис. 1, в) – возникает от ударов колес на стыках, наличия выбоин на одной колесной паре или от неуравновешенности кузова. Галопирование вагона обычно возникает одновременно с подпрыгиванием.
Колебания поперечного относа – кузов и тележка вагона перемещаются вдоль оси у–у (рис. 1, г). Этот вид колебаний возникает совместно с колебаниями боковой качки (рис. 1, д) под действием горизонтальных боковых сил, параллельных оси.
Виляние, когда кузов вращается вокруг вертикальной оси на некоторый угол ±ψ (рис. 1, е), вызывается коничностью поверхности катания колес, неправильной установкой колесных пар, неодинаковой величиной диаметра колес, извилистостью пути.
Подергивание (рис. 1, ж) – перемещение вагона вдоль оси х–х. Оно появляется при трогании поезда с места, торможении вследствие неуравновешенности поступательно движущихся масс локомотива.
Названные колебания могут проявляться отдельно и совместно с другими видами, поэтому вагон совершает сложное движение. Зная причины появления колебаний и их характер, можно определить условия устойчивого и безопасного движения вагона, подобрать рациональные параметры его рессорного подвешивания и поглощающих аппаратов автосцепного устройства. К динамическим характеристикам вагона относятся периоды различных видов колебаний, коэффициенты динамики и критические скорости. В динамике вагонов различают собственные колебания, которые происходят от начального толчка без воздействия в дальнейшем на надрессорное строение каких-либо внешних сил, и вынужденные колебания, возникающие под влиянием периодически меняющейся силы, которую обычно называют возмущающей.
Частота собственных колебаний υc зависит от массы надрессорных частей вагона и жесткости рессорного подвешивания. Частота вынужденных колебаний υв, равна частоте изменений возмущающей силы.
При равенстве частот υв и υc, т. е. при υв:υc = 1, амплитуда колебаний значительно возрастает, наступает явлениерезонанса колебаний, т. е. совпадение периодов свободных колебаний с периодом проявления возмущающей силы. Явление резонанса колебаний характеризуется большими амплитудами или, если применяются ограничивающие колебания устройства, чрезмерно большими силами.Эти силы и перемещения вызывают повышенный износ, а также поломки деталей вагонов и угрожают безопасности движения. Явление резонанса происходит при определенной скорости, которая называется критической. Для гашения колебаний и предотвращения явлений резонанса предусматривается рессорное подвешивание с необходимой величиной коэффициента относительного трения, при которой обеспечивается условие ненарастания колебаний.
где φ – коэффициент относительного трения в рессорном подвешивании;
fст – статический прогиб рессорного подвешивания;
Галопирующие колебания вагона
Галопирующие колебания – это вращательные колебания вокруг горизонтальной оси Y, перпендикулярной бортам вагона и проходящей через центр масс вагона. При этом движение вагона подобно галопу лошади. Колебания обусловлены упругими силами подвески и инертностью вагона.
Пусть из-за случайного толчка, например на стыке рельсов или при падении груза, корпус вагона наклонился. Пусть при этом пружины передней вагонной тележки сжались, а задней тележки – растянулись. Возникает момент упругих сил пружин подвески, стремящийся вернуть вагон в положение равновесия. Но вагон по инерции проходит положение равновесия, поворачиваясь в противоположном направлении. Потом движение повторяется в обратном направлении, и таким образом возникают галопирующие колебания.
Определим период галопирующих колебаний. Так как это вращательные колебания, то для вывода применим основной закон динамики вращательного движения: произведение момента инерции вагона относительно оси вращения на угловое ускорение равно моменту упругих сил подвески: J ε = М.
Получим формулу для момента силы, который создают пружины подвески. По закону Гука упругие силы пружин пропорциональны деформации пружин и направлены противоположно деформации F = –kx. Так как передняя подвеска сжата, то ее сила упругости направлена вертикально вверх, а сила упругости растянутой задней подвески – вниз (рис. 14.4). Момент пары упругих сил подвески F равен произведению силы на плечо пары сил: M = F l, где плечо l равно расстоянию между линиями действия сил, то есть между серединами передней и задней вагонных тележек. Деформация пружин х связана с углом поворота вагона как длина дуги с центральным углом: 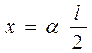
 |
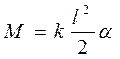
Подставив в закон динамики вращательного движения формулу момента силы, получим дифференциальное уравнение галопирующих колебаний 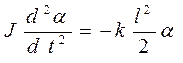
Здесь угловое ускорение записано как вторая производная от угла поворота по времени. Решением этого дифференциального уравнения должна быть функция, у которой вторая производная имеет такой же вид, как и сама функция, но противоположного знака. Например, это может быть функция косинуса
где α0 – амплитуда колебаний, ω – циклическая частота колебаний. Если определить вторую производную от угла поворота по времени 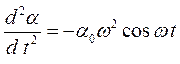
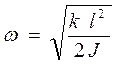
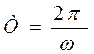
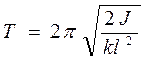
Здесь k –– коэффициент упругости пружин подвески, принятый одинаковым для передней и задней вагонных тележек, J – момент инерции вагона.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
9.8 Взаимодействие вагонов и пути
Взаимодействие вагонов и пути — одна из основных научных технических дисциплин железнодорожного транспорта, имеющая большое практическое значение. Основные объекты исследований этой дисциплины — конструкции пути и вагонов и параметры этих конструкций.
Изучение процессов взаимодействия вагонов и пути началось вместе с зарождением железнодорожного транспорта, поскольку результаты исследований их взаимодействия необходимы для создания надежных и долговечных конструкций вагонов и пути, определения норм их устройства, правил ремонта и технического содержания. Дисциплина включает в себя исследования плоских и пространственных колебаний вагонов при движении их по детерминированным и случайным (стохастическим) неровностям пути; деформаций и необходимых конструктивных размеров элементов вагонов и пути с целью обеспечения достаточной прочности, долговечности, надежности в эксплуатации.
Изучение процессов взаимодействия вагонов и пути началось вместе с зарождением железнодорожного транспорта, поскольку результаты исследований их взаимодействия необходимы для создания надежных и долговечных конструкций вагонов и пути, определения норм их устройства, правил ремонта и технического содержания. Дисциплина включает в себя исследования плоских и пространственных колебаний вагонов при движении их по детерминированным и случайным (стохастическим) неровностям пути; деформаций и необходимых конструктивных размеров элементов вагонов и пути с целью обеспечения достаточной прочности, долговечности, надежности в эксплуатации.
Исследования взаимодействия вагонов и пути являются научной базой рационального конструирования и эксплуатации вагонов и железнодорожного пути и средством интенсификации их использования, повышения пропускной и провозной способности железных дорог, обеспечения безопасности движения с точки зрения устойчивости колеса на рельсе и устойчивости от поперечного опрокидывания кузова вагона в кривых. Для выбора рациональных параметров вагонов при их проектировании, разработки норм размещения перевозимых грузов в вагонах; решения вопросов безопасности движения и повышения прочности и надежности узлов вагонов; определения конструктивной скорости движения вагонов; уменьшения силового воздействия вагонов на путь; обеспечения плавности хода, в частности пассажирских вагонов; уменьшения механического воздействия на перевозимые в грузовых вагонах грузы и соблюдения требований ездового комфорта пассажиров необходимо правильно и точно описать качественно и количественно динамические процессы, происходящие в движущемся вагоне, и управлять этими процессами.
Эту часть дисциплины о взаимодействии вагонов и пути, в которой сконцентрирована совокупность методов и приемов решения задач по качественному и количественному описанию динамических процессов в вагоне и рекомендаций по улучшению динамических показателей вагонов, называют динамикой вагона.
При проектировании конструкций железнодорожного пути и его элементов с выбором их геометрических форм, показателей прочности и надежности, с определением наибольших скоростей движения вагонов и их осевых нагрузок; норм устройства и содержания пути используется совокупность знаний, которая называется динамикой железнодорожного пути и теорией его проектирования и эксплуатации.
Основой обоих направлений взаимодействия вагонов и пути является область исследований или расчетов, которая рассматривает вагон и путь как единую механическую систему. После решения вопросов в общем плане в ряде случаев удается рассматривать изолированно с известной мерой допущения вопросы теоретической механики, относящиеся к вагону или к пути.
Наука о взаимодействии вагонов и пути служит для обеспечения безопасной перевозки грузов и пассажиров в кратчайшие сроки с минимальными затратами материалов на создание и эксплуатацию вагонов. Обеспечение безопасности движения поездов, надежности работы вагонов и пути с их максимальной производительностью и с минимальными затратами труда и энергии, особенно при высоких скоростях движения (свыше 250 км/ч для пассажирских поездов), осевых нагрузках до 30 т и погонных нагрузках до 10—12 т/м для грузовых поездов, при грузонапряженности отдельных линий свыше 200 млн т-км брутто в год, не может быть осуществлено без знания процессов взаимодействия пути и вагонов, которые в конечном итоге сводятся к взаимосвязанным случайным колебаниям различных элементов вагонов и пути, при которых могут возникнуть значительные остаточные деформации пути или потеря устойчивости вагонов на рельсах, усталостные или хрупкие поломки элементов или деталей вагонов и пути. Поэтому умение прогнозировать и рассчитывать, в зависимости от конструктивных особенностей вагонов, скоростей движения, норм содержания пути и вагонов и отступлений от них, грузонапряженности и ряда других факторов, процессы случайных колебаний вагонов и их эволюцию по мере износа пути и вагонов во всех звеньях единой механической системы «вагон — путь», умение управлять этими процессами и составляет конечную цель науки о взаимодействии вагонов и пути.
При этом управление указанными процессами не предусматривает обязательного сведения их к нулю, поскольку это на практике невозможно. Нужно лишь стремиться свести их к такому разумному минимуму, который обеспечивает технические требования к данной системе с учетом перспективы ее эксплуатации и не требует чрезмерных затрат на ее создание и эксплуатацию.
В настоящее время многие важные для железнодорожного транспорта задачи науки о взаимодействии вагонов и пути уже решены или успешно решаются для большей части практических проблем с использованием современных достижений в механике, математике и кибернетике, что позволило в буквальном смысле провести революцию в этой научной дисциплине.При изучении процессов взаимодействия вагонов и пути исследуются колебания вагонов и пути и динамические силы, развивающиеся в единой динамической системе «вагон—путь». Для теоретического исследования колебаний вагона и пути принято строить такие расчетные схемы и модели, в которых этот сложный колебательный процесс разделен на отдельные составляющие его линейные колебания: вертикальные, поперечные и продольные горизонтальные. При этом следует принимать во внимание, что обрессоренная масса вагона (рама тележки, кузов с грузом) может совершать также и угловые колебания.
К вертикальным линейным колебаниям вагона относятся подпрыгивание и галопирование, а к горизонтальным поперечным колебаниям — виляние, боковая качка и поперечный относ кузова на рессорном подвешивании.
Подпрыгивание — это вертикальные одинаковые по величине в каждый момент времени поступательные перемещения всех точек вагона или его обрессоренной массы (кузов, рама тележки).
Галопирование — это вертикальные перемещения точек вагона, возникающие в результате поворота или вращения кузова вокруг мгновенной горизонтальной поперечной оси вращения, проходящей через центр массы вагона.
Виляние — это поперечные колебания колесных пар, совершающиеся в пределах зазоров между гребнями колес и внутренней гранью головок рельсов, приводящие к извилистому движению вдоль пути колесных пар тележек, кузова.
Колебания относа — это поперечные горизонтальные колебания, при которых в каждый момент времени возникают одинаковые по величине поступательные перемещения кузова или рамы тележки.
Боковая качка — это вращательные движения кузова вагона вокруг мгновенной продольной оси вагона. Горизонтальные продольные по отношению к оси пути колебания вагона называются подергиванием.
Изучение процесса взаимодействия пути и вагонов, а также выполнение инженерных расчетов и исследований сводится к следующему: выбор соответствующей математической модели процесса взаимодействия или его расчетной схемы, определение метода исследования и нахождение метода решения той или иной конкретной задачи, определение исходных данных для расчетов или исследований, т.е. параметров всех элементов, входящих в модель или расчетную схему.
Математическая модель представляет собою систему дифференциальных уравнений, выражающих условия динамического равновесия динамической системы «вагон-путь». По этим уравнениям определяют свойства динамической системы, в частности, ее амплитудно-частотную характеристику, с помощью которой при заданных функциях неровностей пути и неровностей на поверхности качения колес могут быть определены параметры колебаний обрессоренной и необрессоренной масс, которые используются на практике для определения напряженного состояния, прочности, надежности элементов вагона и пути, накопления в них остаточных деформаций, возможного схода вагона с рельсов, для установления допускаемой скорости движения вагона.
В экспериментальных исследованиях взаимодействия вагона и пути определяются механические характеристики вагона и пути, значения наиболее существенных параметров механических процессов во взаимодействующих конструкциях. В основу этих исследований положены комплексные испытания с использованием динамометрического и путеиспытательного вагонов-лабораторий, с помощью которых регистрируются соответствующей электронной измерительной аппаратурой и компьютерами линейные и угловые перемещения обрессоренных и необрессоренных масс вагона; вертикальные и горизонтальные ускорения и динамические силы, действующие на вагон при различной конструкции пути и различных неровностях пути; вертикальные и горизонтальные нагрузки на путь от вагонов, напряжения в элементах вагона и пути.
По результатам испытаний определяется максимально допустимая скорость движения вагонов по пути с различными типами верхнего строения и различным планам линии (прямые, кривые) при наличии различных отступлений от проектных норм устройства пути и ходовых частей вагона. В комплексных испытаниях изучается также влияние на динамические процессы различных вариантов конструктивных решений в ходовых частях вагона.
Колебания вагона на рессорном подвешивании
Колебания вагонов, как известно, возникают потому, что колесные пары при своем движении по рельсам и стрелочным переводам совершают сложные пространственные перемещения и тем самым заставляют колебаться на рессорном подвешивании рамы тележек, раму кузова, кузов и сам путь. Таким образом, колебания вагона начинаются с колесной пары и передаются всем остальным деталям вагона и пути. Поэтому и следует рассмотреть вопрос о том, почему зарождаются колебания колеса.
Рассмотрим, прежде всего, вертикальные колебания одной колесной пары.
Фактическая траектория движения колеса определяется геометрическими формами рельса, в частности, его остаточным изгибом, неровностями на поверхности катания, зазорами между рельсами и шпалами, шпалами и балластом и т.п. Образец фактического продольного профиля пути, снятого весьма точной нивелировкой с определением высот точек на поверхности головки рельса приведен на рис. 1. Однако в системе таких неровностей всегда имеются, так называемые, «единичные» неровности, вызванные такими причинами, как одиночно просевшая шпала, крестовина на стрелочном переводе, пробоксовина (местный износ из-за боксования) на рельсе, зимой местное вспучивание пути (пучинa) и т. п. Кроме того, на пути имеются, так называемые «регулярные» неровности. К ним, прежде всего, относятся неровности, возникающие в рельсовых стыках.
При движении вагона по звеньевому пути, т.е. пути, состоящему из отдельных рельсов, соединенных в стыках накладками, всегда возникают соударения колес с рельсами.
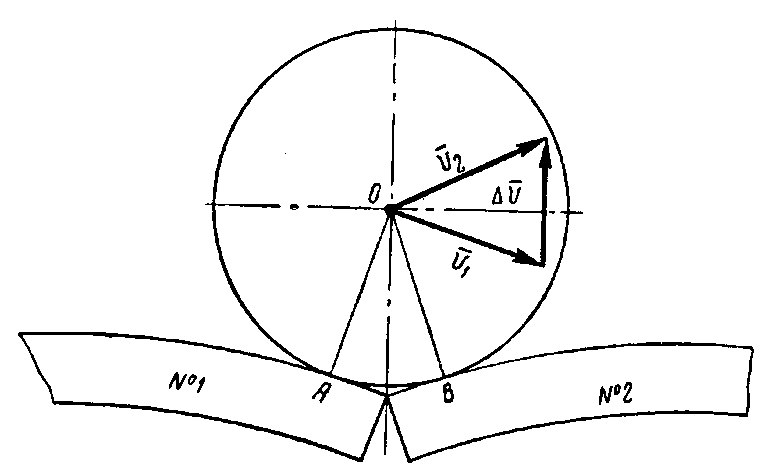
Рассмотрим схематически этот процесс. Из-за того, что изгибная жесткость накладок, соединяющих концы рельсов, меньше изгибной жесткости рельса, прогиб пути в стыке под нагрузкой всегда больше прогиба в средней части рельсового звена. Поэтому, если колесо движется со скоростью v, то оно в последний момент движения по рельсу №1, не доходя до его конца, начинает вращаться вокруг точки А, как вокруг мгновенного центра вращения; при этом вектор скорости v1 направлен перпендикулярно линии АО (рис.2).
В момент контакта колеса в точке В мгновенный центр вращения сразу же скачком (за время dt) перемещается в точку В и вектор скорости колеса v2 получает направление, перпендикулярное линии ОВ. Таким образом, колесо мгновенно изменяет скорость с v1 на v2, т.е. изменение скорости равно вектору
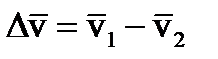
Если масса колеса равна т, то значит за какой-то отрезок времени dt количество движения колеса изменится на величину 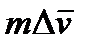
Из теоретической механики известно, что изменение количества движения тела за время dt равно импульсу сил, сообщенному телу за то же время, т. е.
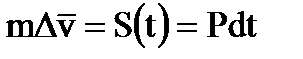
где S(t) — мгновенный ударный импульс;
Р — сила, возникающая при этом импульсе.
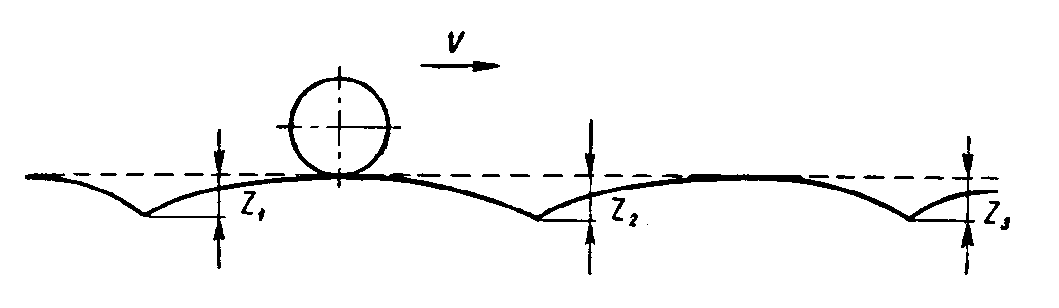
Таким образом, в стыке всегда возникает дополнительная динамическая сила Р, передаваемая и пути и вагону. Для вагона она является источником возникновения колебаний, а для пути — источником повышения просадок шпал в балласте.
В результате возникновения этих просадок продольный профиль пути приобретает вид, показанный на рис. 3.
Совершенно очевидно, что при таком продольном профиле пути колесо вынуждено неравномерно во времени перемещаться в пространстве, что приводит к силам инерции колеса, передаваемым через связи колеса с тележкой другим элементам вагона и пути. Естественно, что это также является одной из причин возникновения колебаний вагонов. К этому следует добавить, что ударные процессы возникают на каждом колесе одной колесной пары не одновременно из-за различного износа стыков, различия в их прогибах и сдвижке стыков друг относительно друга по длине пути.
Траектории движения колес одной колесной пары по просевшим стыкам различны потому, что остаточные просадки разных стыков не одинаковы. Поэтому наряду с вертикальными перемещениями каждого колеса колесная пара из-за различия в этих перемещениях совершает угловые перемещения (рис. 4). Соответствующая неровность рельсового пути носит название «перекос».
Помимо вертикальных неровностей, рельсовый путь также характеризуется горизонтальными неровностями: уширением колеи и отклонением средней линии от оси пути.
Колебания вагона возникают и из-за неравномерного износа поверхности катания колеса (рис. 5) или эксцентричного его положения на оси (рис. 6). В самом деле, при качении изношенного колеса, имеющего различные радиусы качения в разных точках, центр колеса О будет совершать непрерывные колебания, передаваемые кузову вагона. Совершенно аналогичную картину наблюдают и при движении колеса, установленного на оси с эксцентриситетом е.
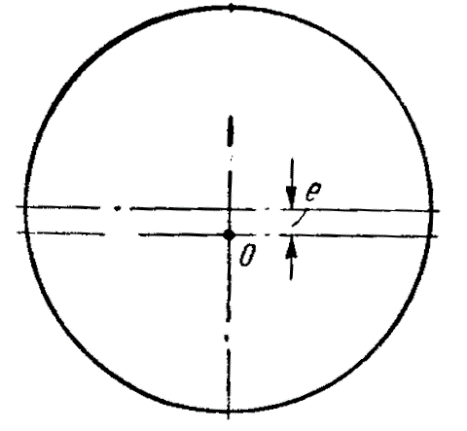
Одной из причин колебаний вагона является его виляние (извилистое движение). Как известно, между гребнями колес и рабочими гранями рельсов существуют зазоры, за счет вторых колесная пара при своем движении может постепенно переходить от контактирования гребнем правого колеса с правым по ходу рельсом к контактированию гребнем левого колеса с левым рельсом.
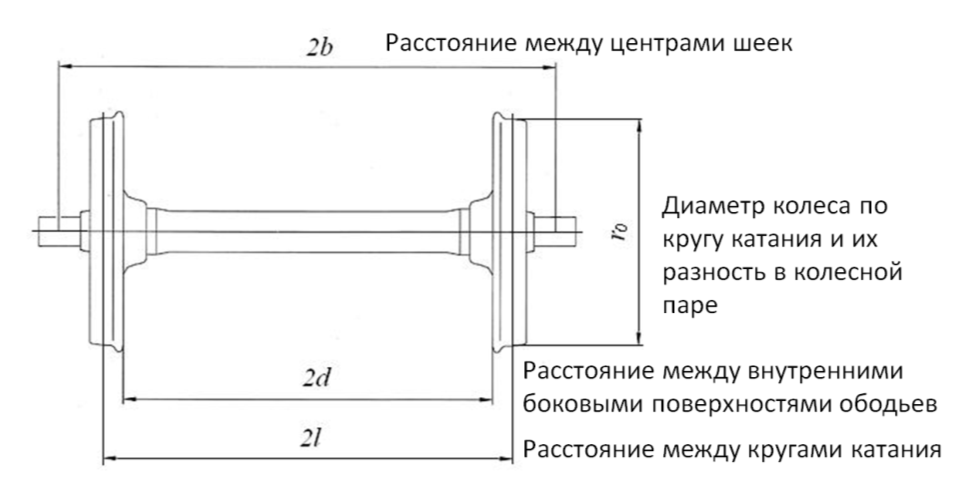
Характеристики колесной пары:
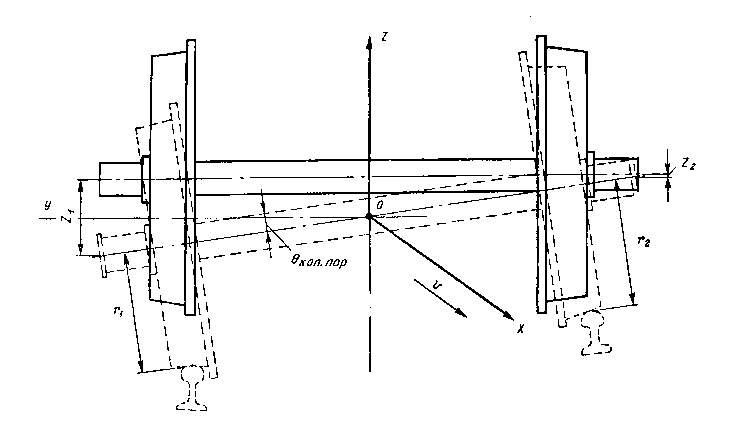
Для обеспечения безопасности движения поездов и снижения сил взаимодействия колеса и рельса относительное расположение рельсов должно отвечать особенностям конструкции ходовых частей подвижного состава. Расположение колесной пары в рельсовой колее показано на рис. 8.
Подуклонка рельсов. Поскольку поверхности катания новых колес имеют уклон 1/20, то и рельсы устанавливаются с наклоном внутрь колеи равным 1/20. Этим достигается большая центрированность опирания бандажа на головку рельса, и за счет этого некоторое снижение напряжений в рельсе и уменьшение пластических деформаций в его головке.
Рис. 8. Схема расположения колесной пары в рельсовой колее
Колесная колея – расстояние между поверхностями гребней колесной пары, измеренное на расстоянии 18 мм от их вершины.
Размеры колесной колеи с учетом допусков на изготовление и износ для колесных пар грузовых/пассажирских вагонов меняются в пределах, указанных в таблице.
| Основные размеры, мм | max | min | Номинал |
| Толщина гребня | 33/33 | 25/25 | 33/33 |
| Насадка колес | 1443/1443 | 1437/1439 | 1440 /1440 |
| Колесная колея | 1509/1509 | 1487/1489 | 1506/1506 |
Примечание. Разница в заштрихованных ячейках появляется только для колесных пар, предназначенных для скорости более 33,0 м/с (120 км/ч).
Рельсовая колея – расстояние между головками рельсов, измеренное в плоскости, лежащей па 13 мм ниже плоскости, проходящей через верхнюю точку поверхности катания рельсов. Стандартный размер ширины колеи после сужения, мм – 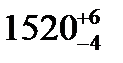
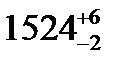
В кривых для обеспечения свободного прохода многоосных экипажей ширина колеи больше, чем в прямых (если 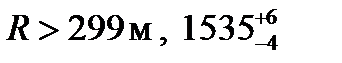
Определим величину зазоров между рабочими гранями гребней и боковыми гранями головок рельсов для прямых участков пути.
Минимальный зазор 1516-1509=7 мм (1522-1509=13 мм).
Номинальный зазор 1520-1506=14 мм (1524-1506=18 мм).
Максимальный зазор 1526-1487=39 мм (1526-1487=43 мм).
Вследствие изгиба оси и отжатия головки рельса под действием поперечных сил величина зазора может быть больше приведенных величин. Дополнительное уширение колеи за счет отжатия рельса может достигать 3 – 5 мм. За счет изгиба оси колесной пары зазор между гребнями колес и головками рельсов увеличивается на 1 – 2 мм.
За счет конической поверхности катания при движении по прямой колесная пара описывает синусоиду (извилистое движение). При этом она касается гребнем рельса с одной стороны.
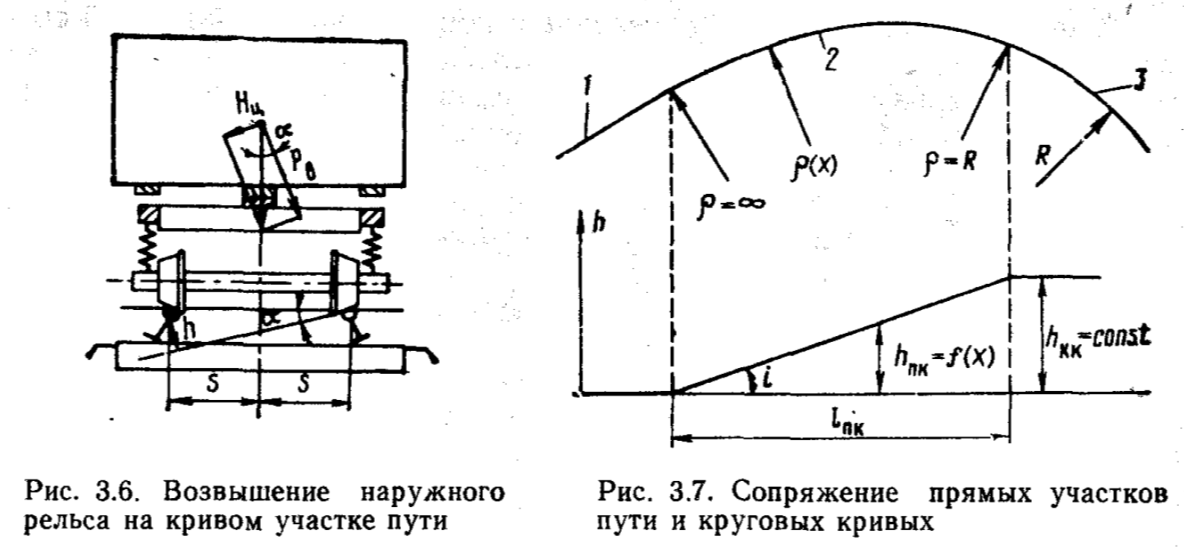
В кривых, очевидно, колесная пара прижимается гребнем к наружному рельсу под действием ускорения. При прижатии гребень трется о рельс.
Поскольку колесная пара при движении непрерывно перемещается поперек колеи (в пределах указанного выше зазора), то ось колесной пары при конической форме колес совершает угловые колебания (см. рис. 4) вокруг оси х (угол j), шейки оси то поднимаются, то опускаются на некоторую величину z. Эти колебания также передаются затем другим элементам вагона.
Колебания вагонов вызываются также действием сил, возникающих при входе вагона в кривые участки пути и в стрелочные кривые, от порывов ветра, аэродинамических толчков воздуха в боковую поверхность вагонов при встрече поездов по некоторым другим причинам.
Виды колебаний вагона в заданной системе координат. Основные понятия.
Расчетную схему вагона с двухступенчатым подвешиванием можно представить в виде, показанном на рис.. Колебания кузова по обобщенным координатам – виды колебаний – имеют следующие общепринятые названия:
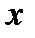
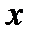
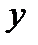
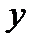
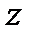
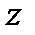
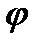
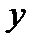
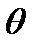
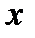
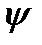
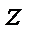
Без индекса координаты относящиеся к кузову, с индексом 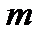
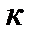
Рис. Расчетная схема вагона с двухступенчатым подвешиванием
Напомним вначале некоторые основные понятия из теории колебаний. В линейных колебательных системах известны два вида колебаний: собственные и вынужденные.
Собственные колебания происходят в изолированных колебательных системах вследствие какого-либо начального возмущения; в процессе самих собственных колебаний никакие внешние дополнительные возмущения на систему не действуют.
Обычно собственные колебания из-за наличия сопротивлений среды с течением времени затухают (прекращаются). Системы, в которых энергия колебаний расходуется на преодоление сопротивлений среды, называют диссипативными, а системы, у которых энергия в окружающую среду не рассеивается — консервативными.
Вынужденные колебания в колебательных системах возникают тогда, когда на систему все время действуют возмущающие силы.
Полнее всего изучены, так называемые, гармонические колебания систем, которые описываются обычно уравнением
где z — величина перемещений в колебательном процессе;
A — амплитуда колебаний;’
vt+a — фаза колебаний;
v — угловая частота колебаний;
a — начальная фаза колебаний.
Напомним, что периодом колебаний Т (в сек) называют промежуток времени, за который какой-то элемент системы совершает полный цикл колебаний, после которого движение повторяется. Очевидно, это будет тогда, когда фаза колебаний изменяется на 2p, т. е. v(t + T) + a = vt + a + 2p.
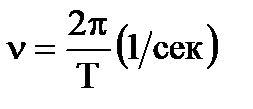
Таким образом, угловой частотой колебаний называется угол (в радианах), на который изменяется фаза за время одного периода. Иногда рассматривают линейную частоту колебаний, т. е. количество периодов колебаний, происходящих в одну секунду, или
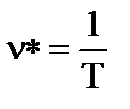
Из формул (1.4) и (1.5) следует, что
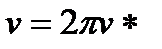
Дата добавления: 2016-12-27 ; просмотров: 3243 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ