Вычислительная ошибка это что
Приложение А. Погрешности вычислений
Абсолютная и относительная погрешности
Точность полученного в результате вычисления результата определяется погрешностью вычислений. Различают два вида погрешностей – абсолютную и относительную.
Абсолютная погрешность некоторого числа равна разности между его истинным значением и приближенным значением, полученным в результате вычисления или измерения:
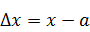
где а – приближенное значение числа х.
Относительная погрешность – это отношение абсолютной погрешности к приближенному значению числа:
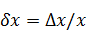
Истинное значение величины х обычно неизвестно. Имеется лишь приближенное значение а и нужно найти его предельную погрешность 

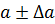
Источники погрешностей
Рассмотрим различные причины возникновения погрешностей.
Математическая модель задачи является неточной
Погрешность возникает из-за того, что сам численный метод или математическая модель является лишь приближением к точному методу (например, дифференцирование). Кроме того, любая математическая модель или метод могут внести существенные погрешности, если в ней не учтены какие-то особенности рассматриваемой задачи. Модель может прекрасно работать в одних условиях и быть совершенно неприемлемой в других. Такую погрешность называют также методической. Она всегда имеет место, даже при абсолютно точных данных и абсолютно точных вычислениях. В большинстве случаев погрешность численного метода можно уменьшить до требуемого значения за счет изменения параметров метода (например, уменьшением шага дискретизации, или увеличением количества итераций).
Ошибки в исходных данных
Исходные данные задачи часто являются основным источником погрешностей. Ошибки такого типа неизбежны и проявляются в любых реальных задачах, поскольку любое измерение может быть проведено с только какой-то предельной точностью. Вместе с погрешностями, вносимыми математической моделью, их называют неустранимыми погрешностями, поскольку они не могут быть уменьшены ни до начала решения задачи, ни в процессе ее решения.
Следует стремиться к тому, чтобы все исходные данные были примерно одинаковой точности. Сильное уточнение одних исходных данных при наличии больших погрешностей в других не приводит к повышению точности конечных результатов. Если какие-то отдельные точки данных (измерения) явно ошибочные, их можно исключить из вычислений.
Вычислительные ошибки (ошибки округления)
Ошибки этого типа проявляются из-за дискретной (а не непрерывной) формы представления величин в компьютере. Вычислительные ошибки можно свести к минимуму продуманно организовывая алгоритмы.
Вычислительные ошибки
Рассмотрим подробнее вычислительные ошибки. Допустим, исходные данные не имеют погрешности, но поскольку место в памяти компьютера, отведенное на хранение чисел, ограничено, и соответственно ограничена точность представления чисел, возникновение вычислительных ошибок неизбежно.
Представление чисел с плавающей точкой
Для хранения целых чисел (int, long, unsigned int и т.д.) обычно отводится 4 байта памяти, что позволяет представлять целые числа, находящиеся примерно в диапазоне от 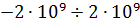
В вычислениях чаще используются вещественные числа (float, double). Такие числа представляются в компьютере в форме с плавающей точкой, и хранятся в логарифмическом виде – мантисса и порядок:
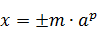
где m – мантисса, p – порядок, а – основание степени.
Например, число 273.9 можно 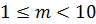
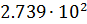
В таблице А.1 приводится диапазон допустимых значений и другие параметры для чисел с плавающей точкой одинарной (float) и двойной (double) точности.
| Точность | Одинарная | Двойная |
| Размер (байты) | 4 | 8 |
| Наименьшее значение | 1.2·10 −38 | 2.3·10 −308 |
| Наибольшее значение | 3.4×10 +38 | 1.7×10 +308 |
| Размеры степени и мантиссы (биты) | 8-23 | 11-52 |
Таблица A.1. Диапазон чисел, представимых в формате с плавающей точкой
Для чисел с плавающей точкой существует понятие машинного эпсилон – наименьшего положительного число ε такого, что 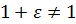
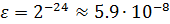
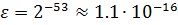
Погрешность округления
При вычислениях с помощью компьютера неизбежны погрешности округлений, связанные с ограниченностью хранимых разрядов мантиссы. Для приближенного числа, полученного в результате округления, абсолютная погрешность 
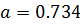
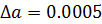
Перевод чисел из одной системы счисления в другую также может быть источником погрешности из-за того, что основание одной системы счисления не является степенью основания другой (например, 10 и 2). Это может привести к тому, что в новой системе счисления число невозможно представить абсолютно точно, например:
Погрешность арифметических действий над приближенными числами
При выполнении операций над приближенными числами можно оценить предельную погрешность результата в зависимости от выполняемой операции. При умножении или делении чисел друг на друга их относительные погрешности складываются:
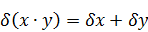
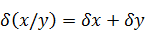
При возведении в степень приближенного числа его относительная погрешность умножается на показатель степени:
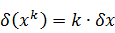
При сложении или вычитании чисел их абсолютные погрешности складываются:
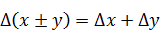
Относительная погрешность суммы положительных слагаемых вычисляется как:
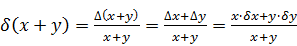
Отсюда следует, что относительная погрешность суммы нескольких чисел одного и того же знака, заключена между наименьшей и наибольшей из относительных погрешностей слагаемых:
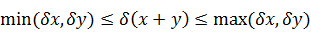
На практике для оценки погрешности при сложении чисел обычно используют максимальную погрешность 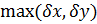
При сложении погрешность будет сильно завесить от абсолютных величин складываемых чисел. Рассмотрим пример сложения двух чисел с одинаковым количеством значащих цифр, но разных по абсолютному значению:
1234 + 0.005678 = 1234.00005678
или в компьютерном представлении:
1.234Е+03 + 5.678Е-03 = 1.234005678Е+03
После сложения количество значащих цифр равно 10. Число с одинарной точностью (float) позволяет хранить только 8 значащих цифр, то есть на самом деле число будет равно 1.2340056Е+03. Две значащие цифры потерялись в процессе сложения. Потеря точности здесь возникает из-за того, что при прибавлении к большому числу малых чисел результат сложения выходит за пределы точности при округлении. Для того чтобы уменьшить погрешность вычислений, нужно складывать числа в порядке возрастания их абсолютной величины. Таким образом можно минимизировать абсолютную величину промежуточной погрешности при каждом сложении.
Рассмотрим теперь вычитание чисел (сложение чисел разного знака, или вычитание чисел одного знака). В соответствии с выражением (А.7) относительная погрешность может быть очень большой в случае, если числа близки между собой, так как даже при малых погрешностях 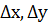
Таким образом, можно сделать вывод, что сложение и вычисление являются плохо обусловленными (неустойчивыми) операторами, так как при некоторых данных даже небольшая погрешность в исходных данных может привести к большой погрешности результата. Уменьшить погрешность можно за счет правильной последовательности операций. Из-за погрешности округления в машинной арифметике важен порядок выполнения операций, и известные из алгебры законы коммутативности (и дистрибутивности) здесь не всегда выполняются.
Классификация ошибок, влияющих на снижение оценки
При проверке математических знаний следует различать грубые и негрубые ошибки.
К грубым ошибкам относятся:
-Вычислительные ошибки в заданиях;
-Ошибки в определении порядка выполнения арифметических действий;
-Неправильное решение задачи (пропуск действий (действия)), неправильный подбор действий (действия), лишние действия;
-Незаконченное решения задачи или примера;
-Невыполненное задание (не приступил к его выполнению) ;
-Незнание или неправильное применение свойств, правил, алгоритмов, существующих зависимостей, которые лежат в основе задач или используются в ходе их выполнения;
-Несоответствие пояснительного текста, задания, названия величин выполненным действиям и полученным результатам;
-Несоответствие выполненных измерений и геометрических построений данным параметрам задачи.
Негрубыми ошибками являются:
-Нерациональные приемы вычисления, если ставились требования воспользоваться такими приёмами;
-Неправильное построение или постановка вопросов к действиям (действия) при решении задачи;
-Неправильное или неграмотное с точки зрения стилистики или по содержанию формулировки ответа задачи;
-Неправильное списывание данных (цифр, знаков) задачи с правильным ее решением;
-Не закончено (не доказано) до логического конца преобразования;
-Ошибки в записях математических терминов, символов;
-Отсутствие ответа в задании или ошибки в записи ответа.
Две негрубым ошибки считают одной грубой ошибки.
Опрятные исправления являются недостатками работы.
За грамматические ошибки, допущенные в работе, оценка по математике не снижается.
За неаккуратно оформленную работу оценка по математике может быть снижена на 1 балл, но не ниже «3», и не в контрольной работе.
Продолжительность выполнения проверочных письменных работ: во 2-м классе начальной школы: I семестр — до 20 мин, II семестр — до 30 мин, 3 — 4-й классы — до 35 мин. За это время ученикам нужно успеть не только полностью выполнить работу, но и проверить ее.
Работа, состоящая из примеров
| Отметка | Характеристика учебных достижений обучающихся |
| Ученикдопускает 4 и более грубых ошибок. | |
| Ученикдопускает 2–3 грубые и 1–2 негрубые ошибки или 3 и более негрубых ошибки. | |
| Ученикдопускает 1 грубую и 1–2 негрубыеошибки. | |
| Ученик выполняет работубез ошибок. |
Работа, состоящая из задач
| Отметка | Характеристика учебных достижений обучающихся |
| Ученикдопускает 2 и более грубых ошибки. | |
| Ученикдопускает 1 грубую и 3–4 негрубыеошибки, правильно выполнено не менее 50% работы. | |
| Ученикдопускает 1 грубую и 1–2 негрубыеошибки. | |
| Ученик выполняет работубез ошибок. |
Комбинированная работа (1 задача, примеры и задание другого вида)
| Отметка | Характеристика учебных достижений обучающихся |
| Ученикдопускает ошибки в ходе решения задачи и хотя быодна вычислительная ошибка или при решении задачи и примеров допущено более 5вычислительных ошибок. | |
| Ученикдопускает ошибки в ходе решения задачи при правильном выполнении всехостальных заданий или допущены 3-4 вычислительные ошибки, при этом ходрешения задачи должен быть верным. | |
| Ученикдопускает 1-2 вычислительные ошибки. | |
| Ученик выполняет работубез ошибок и исправлений. |
Контрольная работа диагностического характера
Егор Вышегородцев | Ошибки танцевальных пар, влияющие на судейскую оценку
Ошибки вычислений
Материал из MachineLearning.
Содержание
Введение
Постановка вопроса. Виды погрешностей
Процесс исследования исходного объекта методом математического моделирования и вычислительного эксперимента неизбежно носит приближенный характер, так как на каждом этапе вносятся погрешности. Построение математической модели связано с упрощением исходного явления, недостаточно точным заданием коэффициентов уравнения и других входных данных. По отношению к численному методу, реализующему данную математическую модель, указанные погрешности являются неустранимыми, поскольку они неизбежны в рамках данной модели.
При переходе от математической модели к численному методу возникают погрешности, называемые погрешностями метода. Они связаны с тем, что всякий численный метод воспроизводит исходную математическую модель приближенно. Наиболее типичными погрешностями метода являются погрешность дискретизации и погрешность округления.
При построении численного метода в качестве аналога исходной математической задачи обычно рассматривается её дискретная модель. Разность решений дискретизированной задачи и исходной называется погрешностью дискретизации. Обычно дискретная модель зависит от некоторого параметра (или их множества) дискретизации, при стремлении которого к нулю должна стремиться к нулю и погрешность дискретизации.
Дискретная модель представляет собой систему большого числа алгебраических уравнений. Для её решения используется тот или иной численный алгоритм. Входные данные этой системы, а именно коэффициенты и правые части, задаются в ЭВМ не точно, а с округлением. В процессе работы алгоритма погрешности округления обычно накапливаются, и в результате, решение, полученное на ЭВМ, будет отличаться от точного решения дискретизированной задачи. Результирующая погрешность называется погрешностью округления (вычислительной погрешностью). Величина этой погрешности определяется двумя факторами: точностью представления вещественных чисел в ЭВМ и чувствительностью данного алгоритма к погрешностям округления.
Виды мер точности
Мерой точности вычислений являются абсолютные и относительные погрешности. Абсолютная погрешность определяется формулой
В общем случае абсолютная погрешность должна удовлетворять следующему неравенству:
Относительная погрешность связана с количеством верных цифр приближенного числа соотношением:
Так как точное решение задачи как правило неизвестно, то погрешности приходится оценивать через исходные данные и особенности алгоритма. Если оценка может быть вычислена до решения задачи, то она называется априорной. Если оценка вычисляется после получения приближенного решения задачи, то она называется апостериорной.
Очень часто степень точности решения задачи характеризуется некоторыми косвенными вспомогательными величинами. Например точность решения системы алгебраических уравнений
Предельные погрешности
Можно показать, что при малых эта оценка не может быть существенно улучшена. На практике иногда пользуются грубой (линейной) оценкой
Несложно показать, что:
Погрешности округлений при представлении чисел в компьютере
Абсолютная погрешность округления в этом случае равна
Погрешности арифметических операций
При вычислениях с плавающей точкой операция округления может потребоваться после выполнения любой из арифметических операций. Так умножение или деление двух чисел сводится к умножению или делению мантисс. Так как в общем случае количество разрядов мантисс произведений и частных больше допустимой разрядности мантиссы, то требуется округление мантиссы результатов. При сложении или вычитании чисел с плавающей точкой операнды должны быть предварительно приведены к одному порядку, что осуществляется сдвигом вправо мантиссы числа, имеющего меньший порядок, и увеличением в соответствующее число раз порядка этого числа. Сдвиг мантиссы вправо может привести к потере младших разрядов мантиссы, т.е. появляется погрешность округления.
Рассмотрим трансформированные погрешности арифметических операций. Арифметические операции проводятся над приближенными числами, ошибка арифметических операций не учитывается (эту ошибку легко учесть, прибавив ошибку округления соответствующей операции к вычисленной ошибке).
Рассмотрим сложение и вычитание приближенных чисел. Абсолютная погрешность алгебраической суммы нескольких приближенных чисел равна сумме абсолютных погрешностей слагаемых.
Если сумма точных чисел равна
сумма приближенных чисел равна
Относительная погрешность суммы нескольких чисел равна
Из (2) следует, что относительная погрешность суммы нескольких чисел одного и того же знака заключена между наименьшей и наибольшей из относительных погрешностей слагаемых:
0.» alt= «min \quad \delta(a_k)\le\delta(S)\le max \quad \delta(a_k), \qquad k=1,2. n, \quad a_k>0.» />
При сложении чисел разного знака или вычитании чисел одного знака относительная погрешность может быть очень большой (если числа близки между собой). Так как даже при малых величина может быть очень малой. Поэтому вычислительные алгоритмы необходимо строить таким образом, чтобы избегать вычитания близких чисел.
Необходимо отметить, что погрешности вычислений зависят от порядка вычислений. Далее будет рассмотрен пример сложения трех чисел.
При другой последовательности действий погрешность будет другой:
Из (3) видно, что результат выполнения некоторого алгоритма, искаженный погрешностями округлений, совпадает с результатом выполнения того же алгоритма, но с неточными исходными данными. Т.е. можно применять обратный анализ: свести влияние погрешностей округления к возмущению исходных данных. Тогда вместо (3) будет следующая запись:
При умножении и делении приближенных чисел складываются и вычитаются их относительные погрешности.
При большом числе n арифметических операций можно пользоваться приближенной статистической оценкой погрешности арифметических операций, учитывающей частичную компенсацию погрешностей разных знаков:
где – суммарная погрешность, – погрешность выполнения операций с плавающей точкой,
– погрешность представления чисел с плавающей точкой.
Погрешности вычисления функций
(погрешностью других аргументов пренебрегаем).
Если вклад погрешностей всех аргументов примерно одинаков, то применяют принцип равных влияний:
Числовые примеры
Специфику машинных вычислений можно пояснить на нескольких элементарных примерах.
ПРИМЕР 1. Вычислить все корни уравнения
Точное решение задачи легко найти:
ПРИМЕР 2. Решается задача Коши для обыкновенного дифференциального уравнения 2-го порядка:
Общее решение имеет вид:
ПРИМЕР 3. Пусть необходимо найти решение обыкновенного дифференциального уравнения:
Соответственно, разность будет:
Таким образом, требование к заданию точности начальных данных оказываются в раз выше необходимой точности результата решения задачи. Это требование, скорее всего, окажется нереальным.
Решение оказывается очень чувствительным к заданию начальных данных. Такого рода задачи называются плохо обусловленными.
В памяти машины эти же числа представляются в виде:
Относительная ошибка при вычислении разности будет равна:
ПРИМЕР 6. Рассмотрим рекуррентное соотношение 0, \quad u_i > 0.» alt= «u_
Следовательно, если 1″ alt= «|q| > 1» />, то в процессе вычислений погрешность, связанная с возникшей ошибкой округления, будет возрастать (алгоритм неустойчив). В случае погрешность не возрастает и численный алгоритм устойчив.
Причины вычислительных ошибок младших школьников
Дата публикации: 16.03.2016 2016-03-16
Статья просмотрена: 2577 раз
Библиографическое описание:
Смородинова, Л. В. Причины вычислительных ошибок младших школьников / Л. В. Смородинова. — Текст : непосредственный // Молодой ученый. — 2016. — № 5.6 (109.6). — С. 93-94. — URL: https://moluch.ru/archive/109/27017/ (дата обращения: 12.12.2021).
В статье рассматриваются различные аспекты возникновения вычислительных ошибок младших школьников. Перечислены типы вычислительных ошибок, приведены возможные пути устранения вычислительных ошибок.
Ключевые слова: вычислительные ошибки, содержание ошибок, причины ошибок.
При формировании способов вычислений у младших школьников часто возникают типичные ошибки, поскольку процесс формирования является сложным и длительным. Под типичной вычислительной ошибкой в литературе понимают полученный несколькими учениками результат вычислений, неадекватный объективному (А.К. Артемов, П.Я. Шеварев). Успех обучения зависит от своевременного предупреждения таких ошибок [2]. Это возможно лишь в случае выявления их причин возникновения.
Различные аспекты причин ошибок, допускаемых школьниками, были исследованы в диссертациях Г. А. Асанова, Д.И. Икрамова, И.М. Кирилецкого [4], А.Г. Муханова, В.Г. Прочухаева, Д.А. Скрыпника, А.Ф. Сычикова и др. В этих работах перечислены типы допускаемых ошибок [1]. Приведено большое количество примеров ошибочных рассуждений и связанных с ними неверных решений [2].
Достаточно подробно исследованы отклонения действий учащихся от верных.
В то же время, можно констатировать, что в приведенных источниках предлагается анализ ошибок, проведенный с позиций их содержания. Однако он не гарантирует исчезновения типичных ошибок при дальнейшей работе [3].
Многие исследователи единодушны в том, что чаще всего причина появления ошибки имеет методический характер. Для анализа причин появления типичных ошибок в процессе вычислений воспользуемся методикой, разработанной А.К. Артемовым.
Будем различать содержание ошибки и причину ее возникновения. Содержание ошибки составляет то, что объективно неверно, неадекватно выполнено в действиях учащихся. Причиной ошибки называется некоторое обстоятельство (или их совокупность), повлекшие выполнение неадекватного действия. Например, если учащийся выполняет сложение чисел следующим образом: 54 + 3 = 84, то содержание ошибки составляет нарушение алгоритма сложения двузначного и однозначного чисел (вместо прибавления второго слагаемого к единицам первого слагаемого ученик прибавляет второе слагаемое к десяткам первого слагаемого). Причина ошибки остается пока неясной.
Методика выявления причин ошибок, предложенная названными авторами, предусматривает сопоставление двух ситуаций: той, в которой ученик допустил ошибку, и той, в которой он выполнил верное действие. В качестве последней может быть взят процесс объективно выполненного действия. Эти ситуации должны быть сходны (или различаться) по одному существенному компоненту. При сопоставлении ситуаций сначала устанавливается, какие условия необходимы и достаточны для верно выполненного действия. Затем путем анализа условий обучения выявляются обстоятельства, благоприятствующие зарождению ошибки. Для приведенного примера процесс объективно верного выполнения сложения будет таким: 54+3=(50+4)+3=50+(4+3)=50+7=57. При сопоставлении ошибочно и верно выполненных действий возникают следующие предположения:
− Ученик не заменил двузначное число суммой разрядных слагаемых (причиной этого может служить неполная ориентировочная основа действия сложения двузначного и однозначного чисел).
− Ученик не включил в обобщенную ориентировочную основу действия существенный для сложения признак «можно складывать только величины, измеренные в одних мерках».
Оба предположения указывают на то, что у ученика, совершившего ошибку, сформирована неполная частная ориентировочная основа действия сложения двузначного и однозначного чисел. В этом заключается ближайшая причина возникновения ошибки.
Сформированная неполная частная ориентировочная основа действия может быть причиной слишком узких и слишком широких обобщений. Поясним это утверждение.
Ориентировочная основа действия – это набор ориентиров, необходимый и достаточный для верного выполнения действия или распознавания понятия. Если хотя бы один из ориентиров отсутствует в ООД, действие становится другим и ведет к неверному результату. Если ученик не достраивает самостоятельно сформированную ООД, то будем говорить, что в этом случае ученик владеет слишком широкой ООД.
Таким образом, для предупреждения появления ошибок необходимо не только выявить их содержание, но и определить ближайшие и отдаленные причины возникновения. Результатом этого анализа может быт разработка специальных упражнений с учетом психологических закономерностей процесса усвоения знаний и умений. [6]
