какую окружность называют описанной около треугольника
Окружность, описанная около треугольника
Что такое окружность, описанная около треугольника? Что является центром этой окружности? Как расположение центра описанной окружности зависит от вида треугольника?
Окружность называется описанной около треугольника, если все вершины треугольника лежат на окружности.
Расстояние от любой вершины треугольника до центра описанной окружности равно радиусу этой окружности.
Окружность можно описать около любого треугольника.
Центром описанной около треугольника окружности является точка пересечения серединных перпендикуляров к сторонам треугольника (то есть отрезков, перпендикулярных к сторонам треугольника и проходящих через середины этих сторон).
Центр окружности, описанной около остроугольного треугольника, лежит внутри треугольника.
Центр описанной около прямоугольного треугольника окружности лежит на середине гипотенузы.
Центр окружности, описанной около тупоугольного треугольника, лежит вне треугольника (напротив тупого угла, за большей стороной).
Окружность, описанная около треугольника
Определение окружности, описанной около треугольника
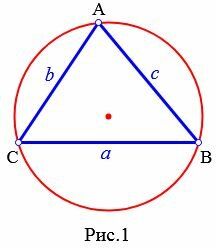
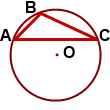
Определение 1. Окружностью, описанной около треугольника называется окружность, проходящей через все три вершины треугольника (Рис.1).
 |
Теорема об окружности, описанной около треугольника
Теорема 1. Около любого треугольника можно описать окружность.
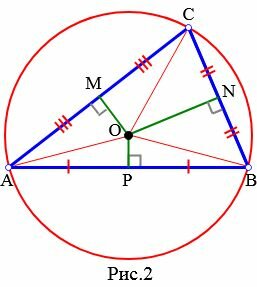 |
Доказательство. Пусть задан произвольный треугольник ABC (Рис.2). Обозначим точкой O точку пересечения серединных перпендикуляров к его сторонам. Проведем отрезки OA, OB и OC. Поскольку точка O равноудалена от точек A, B и C, то OA=OB=OC. Тогда окружность с центром O и радиусом OA проходит через все три вершины треугольника ABC и, следовательно, является окружностью, описанной около треугольника ABC.
Из теоремы 1 следует, что центром описанной около треугольника окружности является точка пересечения серединных перпендикуляров к сторонам треугольника.
Замечание 1. Около любого треугольника можно описать только одну окружность.
Доказательство. Допустим, что около треугольника можно описать две окружности. Тогда центр каждой из этих окружностей равноудален от вершин треугольника и совпадает с точкой O пересечения серединных перпендикуляров сторон треугольника. Радиус этих окружностей равен расстоянию от точки O до вершин треугольника. Поэтому эти окружности совпадают.
Окружность, описанная около треугольника.
Треугольник, вписанный в окружность. Теорема синусов
 Серединный перпендикуляр к отрезку Серединный перпендикуляр к отрезку |
 Окружность описанная около треугольника Окружность описанная около треугольника |
 Свойства описанной около треугольника окружности. Теорема синусов Свойства описанной около треугольника окружности. Теорема синусов |
 Доказательства теорем о свойствах описанной около треугольника окружности Доказательства теорем о свойствах описанной около треугольника окружности |
Серединный перпендикуляр к отрезку
Таким образом, в случае, когда точки E и A лежат по разные стороны от серединного перпендикуляра, мы получили противоречие.
Полученное противоречие и завершает доказательство теоремы 2

















 ,
,



 Окружность с центром в точке O и радиусом R описана около пятиугольника ABCDE.
Окружность с центром в точке O и радиусом R описана около пятиугольника ABCDE.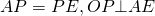
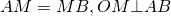
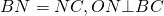
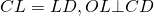
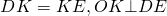
 Точка O равноудалена от вершин пятиугольника.
Точка O равноудалена от вершин пятиугольника.