какую наименьшую длину должна иметь железная проволока чтобы при вертикальном положении
Какую наименьшую длину должна иметь железная проволока, чтобы при вертикальном положении она разорвалась под действием собственного
В 14:50 поступил вопрос в раздел ЕГЭ (школьный), который вызвал затруднения у обучающегося.
Вопрос вызвавший трудности
Ответ подготовленный экспертами Учись.Ru
Для того чтобы дать полноценный ответ, был привлечен специалист, который хорошо разбирается требуемой тематике «ЕГЭ (школьный)». Ваш вопрос звучал следующим образом: Какую наименьшую длину должна иметь железная проволока, чтобы при вертикальном положении она разорвалась под действием собственного
После проведенного совещания с другими специалистами нашего сервиса, мы склонны полагать, что правильный ответ на заданный вами вопрос будет звучать следующим образом:
ответ к заданию по физике
НЕСКОЛЬКО СЛОВ ОБ АВТОРЕ ЭТОГО ОТВЕТА:
Работы, которые я готовлю для студентов, преподаватели всегда оценивают на отлично. Я занимаюсь написанием студенческих работ уже более 4-х лет. За это время, мне еще ни разу не возвращали выполненную работу на доработку! Если вы желаете заказать у меня помощь оставьте заявку на этом сайте. Ознакомиться с отзывами моих клиентов можно на этой странице.
ПОМОГАЕМ УЧИТЬСЯ НА ОТЛИЧНО!
Выполняем ученические работы любой сложности на заказ. Гарантируем низкие цены и высокое качество.
Деятельность компании в цифрах:
Зачтено оказывает услуги помощи студентам с 1999 года. За все время деятельности мы выполнили более 400 тысяч работ. Написанные нами работы все были успешно защищены и сданы. К настоящему моменту наши офисы работают в 40 городах.
Площадка Учись.Ru разработана специально для студентов и школьников. Здесь можно найти ответы на вопросы по гуманитарным, техническим, естественным, общественным, прикладным и прочим наукам. Если же ответ не удается найти, то можно задать свой вопрос экспертам. С нами сотрудничают преподаватели школ, колледжей, университетов, которые с радостью помогут вам. Помощь студентам и школьникам оказывается круглосуточно. С Учись.Ru обучение станет в несколько раз проще, так как здесь можно не только получить ответ на свой вопрос, но расширить свои знания изучая ответы экспертов по различным направлениям науки.
Какую наименьшую длину должна иметь стальная проволока?
Какую наименьшую длину должна иметь свободно подвешенная за один конец стальная проволока, чтобы она разорвалась под действием силы тяжести? Предел прочности стали равен 3,2⋅108 Па, плотность – 7800 кг/м3.
Вычислим силу отрыва, создаваемую стальным кубом размером ребра 1 м, будь он приклеен к потолку.
Определяем удлинение куба вниз при сохранении поперечного сечения в 1 м² до момента его разрыва под собственным весом
L = 3,2⋅10^8/76440=4186 (м).
Обычно в большинстве общеобразовательных школах физика начинается в седьмом классе и по одиннадцатый класс. Но бывает, что физика начинается и с пятого класса. К примеру, по крайней мере существуют учебники физики 5-6 классы.
Для меня любовь до точки, это до того момента, когда любишь человека, причём чувства взаимные, а потом просто этого человека нет. В одно мгновение, в считанные минуты человека просто нет.
Так случилось и в моей жизни. Любимый муж умер от банальной, протекающей бессимптомно пневмонии и ничего не предвещало его ухода, были симптомы простой простуды после ночной, двухдневной рыбалки, причём в конце мая. Вот это я называю, любовь до точки, а ещё можно сказать, что любовь до гроба.
Так же любовь до точки может быть и когда двое любят друг друга и что то вдруг случается(измена, просто быт, который съедает отношения, пьянство и много других причин)и отношения заходят в тупик. А точнее в этой любовной истории можно поставить точку.
Ещё говорят:- От любви, до ненависти один шаг. Это тоже своего рода точка в отношениях. Её можно поставить, когда в семье происходят пьянки, побои, измены, унижения.
Вот и я так считаю, что в настоящей любви точки быть не может, чтоб её поставить нужно или потерять или испытать боль, чтоб потом возненавидеть.
§ 9.15. Примеры решения задач
В задачах на расчет деформаций твердых тел используется понятие напряжения (9.3.1), закон Гука в форме (9.3.2) и (9.3.4), а также понятие предела прочности и запаса прочности (9.3.5).
При решении задач по гидростатике используются основные законы этого раздела: закон Паскаля и закон Архимеда. В этом разделе иногда применяют условия равновесия твердого тела. При рассмотрении равновесия тел в неинерциальных системах отсчета необходимо учитывать силы инерции. Задачи о плавании тел решаются на основе условий равновесия.
Задачи гидродинамики решаются с использованием уравнения Бернулли, но можно решать их, применяя закон сохранения энергии.
Какую силу надо приложить к латунной проволоке длиной l0 = 3 м и площадью сечения S = 1 мм 2 для ее удлинения на Δl = 1,5 мм?
Решение. Согласно закону Гука σ = Еε, где Е = 10 11 Па — модуль Юнга для латуни, σ = 

Закон Гука можно записать в форме
Решение. Зная запас прочности, находим допустимое напряжение σдоп = 
Учитывая запас прочности, получаем:
Решение. Когда шарик висит на пружине в воздухе, то сила упругости пружины уравновешивает силу тяжести, действующую на шарик:
где k — жесткость пружины и V — объем шарика.
На шарик в затопленном состоянии вниз действуют сила тяжести и сила упругости со стороны растянутой пружины. Эти силы уравновешиваются действующей вверх на шарик архимедовой силой:
Разделив почленно (9.15.2) на (9.15.1), получим:
Неоднородная твердая балка BD массой m подвешена на трех одинаковых параллельных тросах, расположенных на равных расстояниях друг от друга. Один из тросов прикреплен в середине балки, а два других — на ее концах. Определите силы реакции тросов, если центр тяжести балки расположен на расстоянии ВК = 
Решение. Обозначим искомые силы через F1, F2, F3. Расстояния между тросами будем считать равными а. Сила тяжести приложена в точке К на расстоянии 
Законы статики дают нам два условия равновесия: равенство нулю суммы проекций сил на ось У:
и равенство нулю суммы моментов этих сил относительно оси, проходящей, например, через точку В:
Мы получили два уравнения с тремя неизвестными. Если считать тросы абсолютно твердыми, как это мы делали в статике, то больше никаких уравнений получить нельзя.
Чтобы найти недостающее уравнение, будем считать тросы упругими телами, подчиняющимися закону Гука. Пусть тросы имеют одинаковую длину, но сделаны из разных материалов и имеют разные площади S1, S2, S3 поперечных сечений. Модули Юнга тросов соответственно равны E1, E2, Е3.
Под действием нагрузки тросы получают абсолютные удлинения Δl1, Δl2, Δl3 (см. рис. 9.53).
Для каждого троса на основании закона Гука можно записать:
где σ1, σ2, σ3 — напряжения в тросах. Учитывая определение напряжения (9.3.1), получим:
Так как BD — прямая линия, то из подобия треугольников ABD и CDE (см. рис. 9.53) можно записать:
Это и есть недостающее третье уравнение. Решите самостоятельно полученную систему трех уравнений первой степени с тремя неизвестными в общем виде.
Мы в соответствии с условием задачи будем считать, что тросы сделаны из одного и того же материала и имеют одинаковые сечения. Тогда получим три следующих уравнения:
Сосуд с жидкостью движется горизонтально с постоянным ускорением а, направленным горизонтально. Как расположится поверхность жидкости? Чему равно давление внутри жидкости в произвольной точке?
Решение. Проще всего решать задачу в неинерциальной системе отсчета, связанной с сосудом. Выделим на поверхности жидкости малый элемент жидкости массой Δm (рис. 9.54, а). В системе отсчета, связанной с сосудом, на выделенный элемент жидкости действуют три силы: сила тяжести Δm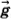



Выделенный элемент жидкости находится в равновесии. Поэтому вектор 

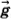

Согласно условию равновесия Δm 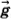


Откуда α = arctg
Обозначим модуль ускорения, создаваемого силой тяжести и силой инерции (рис. 9.55, а), через a1, тогда а1 = 


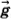

Давление в любой точке В внутри жидкости можно выразить через высоту h до поверхности жидкости по вертикали или через расстояние l до поверхности жидкости по горизонтали. Расстояние от точки В до поверхности жидкости по нормали к ней обозначим через h’ (рис. 9.55, б).
Из прямоугольных треугольников ABD и DBC находим:
(см. рис. 9.55, а). Поэтому
где р0 — давление на поверхность жидкости, ρ — плотность жидкости.
Из (9.15.4) следует, что уровни постоянного давления совпадают с плоскостями, параллельными поверхности жидкости.
Заметим, что при действии силы тяжести и горизонтально направленной силы инерции архимедова сила направлена не вертикально вверх, а по нормали к поверхности жидкости и равна:
На поршень шприца, имеющий площадь S, действует постоянная сила 

Решение. Пусть за время τ поршень перемещается на расстояние uτ (рис. 9.56), где u — модуль скорости поршня. Тогда сила совершает за это время работу А = Fuτ. Масса вытекшей за время τ жидкости равна ρSuτ. Изменение кинетической энергии равно 
Модуль скорости истечения жидкости 

Исключая из двух последних уравнений и, найдем:
Решение. Воспользуемся уравнением Бернулли. Давление в струе воды равно атмосферному р0. Давление под поршнем на высоте h от отверстия равно р0 + 
§ 9.15. Примеры решения задач
В задачах на расчет деформаций твердых тел используется понятие напряжения (9.3.1), закон Гука в форме (9.3.2) и (9.3.4), а также понятие предела прочности и запаса прочности (9.3.5).
При решении задач по гидростатике используются основные законы этого раздела: закон Паскаля и закон Архимеда. В этом разделе иногда применяют условия равновесия твердого тела. При рассмотрении равновесия тел в неинерциальных системах отсчета необходимо учитывать силы инерции. Задачи о плавании тел решаются на основе условий равновесия.
Задачи гидродинамики решаются с использованием уравнения Бернулли, но можно решать их, применяя закон сохранения энергии.
Какую силу надо приложить к латунной проволоке длиной l0 = 3 м и площадью сечения S = 1 мм 2 для ее удлинения на Δl = 1,5 мм?
Решение. Согласно закону Гука σ = Еε, где Е = 10 11 Па — модуль Юнга для латуни, σ = 

Закон Гука можно записать в форме
Решение. Зная запас прочности, находим допустимое напряжение σдоп = 
Учитывая запас прочности, получаем:
Решение. Когда шарик висит на пружине в воздухе, то сила упругости пружины уравновешивает силу тяжести, действующую на шарик:
где k — жесткость пружины и V — объем шарика.
На шарик в затопленном состоянии вниз действуют сила тяжести и сила упругости со стороны растянутой пружины. Эти силы уравновешиваются действующей вверх на шарик архимедовой силой:
Разделив почленно (9.15.2) на (9.15.1), получим:
Неоднородная твердая балка BD массой m подвешена на трех одинаковых параллельных тросах, расположенных на равных расстояниях друг от друга. Один из тросов прикреплен в середине балки, а два других — на ее концах. Определите силы реакции тросов, если центр тяжести балки расположен на расстоянии ВК = 
Решение. Обозначим искомые силы через F1, F2, F3. Расстояния между тросами будем считать равными а. Сила тяжести приложена в точке К на расстоянии 
Законы статики дают нам два условия равновесия: равенство нулю суммы проекций сил на ось У:
и равенство нулю суммы моментов этих сил относительно оси, проходящей, например, через точку В:
Мы получили два уравнения с тремя неизвестными. Если считать тросы абсолютно твердыми, как это мы делали в статике, то больше никаких уравнений получить нельзя.
Чтобы найти недостающее уравнение, будем считать тросы упругими телами, подчиняющимися закону Гука. Пусть тросы имеют одинаковую длину, но сделаны из разных материалов и имеют разные площади S1, S2, S3 поперечных сечений. Модули Юнга тросов соответственно равны E1, E2, Е3.
Под действием нагрузки тросы получают абсолютные удлинения Δl1, Δl2, Δl3 (см. рис. 9.53).
Для каждого троса на основании закона Гука можно записать:
где σ1, σ2, σ3 — напряжения в тросах. Учитывая определение напряжения (9.3.1), получим:
Так как BD — прямая линия, то из подобия треугольников ABD и CDE (см. рис. 9.53) можно записать:
Это и есть недостающее третье уравнение. Решите самостоятельно полученную систему трех уравнений первой степени с тремя неизвестными в общем виде.
Мы в соответствии с условием задачи будем считать, что тросы сделаны из одного и того же материала и имеют одинаковые сечения. Тогда получим три следующих уравнения:
Сосуд с жидкостью движется горизонтально с постоянным ускорением а, направленным горизонтально. Как расположится поверхность жидкости? Чему равно давление внутри жидкости в произвольной точке?
Решение. Проще всего решать задачу в неинерциальной системе отсчета, связанной с сосудом. Выделим на поверхности жидкости малый элемент жидкости массой Δm (рис. 9.54, а). В системе отсчета, связанной с сосудом, на выделенный элемент жидкости действуют три силы: сила тяжести Δm



Выделенный элемент жидкости находится в равновесии. Поэтому вектор 



Согласно условию равновесия Δm 


Откуда α = arctg
Обозначим модуль ускорения, создаваемого силой тяжести и силой инерции (рис. 9.55, а), через a1, тогда а1 = 




Давление в любой точке В внутри жидкости можно выразить через высоту h до поверхности жидкости по вертикали или через расстояние l до поверхности жидкости по горизонтали. Расстояние от точки В до поверхности жидкости по нормали к ней обозначим через h’ (рис. 9.55, б).
Из прямоугольных треугольников ABD и DBC находим:
(см. рис. 9.55, а). Поэтому
где р0 — давление на поверхность жидкости, ρ — плотность жидкости.
Из (9.15.4) следует, что уровни постоянного давления совпадают с плоскостями, параллельными поверхности жидкости.
Заметим, что при действии силы тяжести и горизонтально направленной силы инерции архимедова сила направлена не вертикально вверх, а по нормали к поверхности жидкости и равна:
На поршень шприца, имеющий площадь S, действует постоянная сила 

Решение. Пусть за время τ поршень перемещается на расстояние uτ (рис. 9.56), где u — модуль скорости поршня. Тогда сила совершает за это время работу А = Fuτ. Масса вытекшей за время τ жидкости равна ρSuτ. Изменение кинетической энергии равно 
Модуль скорости истечения жидкости 

Исключая из двух последних уравнений и, найдем:
Решение. Воспользуемся уравнением Бернулли. Давление в струе воды равно атмосферному р0. Давление под поршнем на высоте h от отверстия равно р0 + 














































































