какую фигуру называют квадратом
Квадрат
Это статья о геометрической фигуре. Другие значения слова см. на странице Квадрат (значения)
Квадра́т — правильный четырёхугольник, у которого все углы и стороны равны.
Содержание
Признаки квадрата
1) Равенство длин сторон; 2) Равенство углов (по 90 градусов)
Свойства
Неевклидова геометрия
Многообразие квадратов
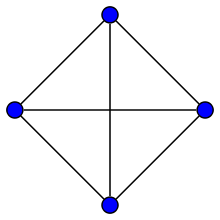
Графы: K4 полный граф часто изображается как квадрат с 6 рёбрами.
Интересное
В виде квадратиков иногда отображаются некоторые символы по причине сложного начертания. Например:឴឴្ឳឲឣបឫឹី៛ݮݯݲݼݳݴඝඟඟදශණඪයරතඡඣ
См. также
Примечания
Ссылки
Полезное
Смотреть что такое «Квадрат» в других словарях:
КВАДРАТ — (лат. quadratum, от quadrare сделать четырехугольным). 1) прямоугольный, равносторонний четырехугольник. 2) такое число, которое, будучи умножено само на себя, дает данное число. 3) единица для измерения плоскостей; напр.: квадратн. фут, дюйм и… … Словарь иностранных слов русского языка
КВАДРАТ — в квадрате. Жарг. мол. Пренебр. О крайне тупом, безнадёжно глупом человеке. /em> Квадрат глупый, несообразительный чаловек. Никитина 1996, 82. Квадрат твою гипотенузу! Жарг. шк. Бран. Выражение досады, раздражения, негодования. ВМН 2003, 62.… … Большой словарь русских поговорок
КВАДРАТ — • КВАДРАТ, в биологии квадратная рама, используемая для разметки участка поверхности с целью изучения растений, находящихся на нем. Квадратом называют также и сам этот участок почвы. Как правило, такой квадрат равен 0,5 или 1 м2. Пользуясь этим… … Научно-технический энциклопедический словарь
КВАДРАТ — КВАДРАТ, квадрата, муж. (лат. quadratus четырехугольный). 1. Равносторонний прямоугольник (мат.). 2. Форма такого прямоугольника у какого нибудь предмета (книжн.). Ярко освещенный квадрат окна. 3. Четырехугольный гартовый брусок мера для… … Толковый словарь Ушакова
КВАДРАТ — муж. равносторонний и прямоугольный четыреугольник; народ называет его круглым четыреугольником или клеткою. Разбить площадь на квадраты, на участки этого вида. | Квадрат числа, произведение его от умножения самого на себя. Узор квадратцами или… … Толковый словарь Даля
КВАДРАТ — в полиграфии, 1) единица длины, применяемая для измерения шрифтов, формата набора. 1 квадрат = 48 пунктам (ок. 18,05 мм).2) Разновидность пробельного материала для заполнения крупных промежутков в строках … Большой Энциклопедический словарь
квадрат — параллелограмм, клетка, материал, прямоугольник, степень, квадратик Словарь русских синонимов. квадрат сущ., кол во синонимов: 9 • гиперкуб (12) • … Словарь синонимов
квадрат — КВАДРАТ, а, м. Тюрьма; камера. квадрат топтать находиться в тюрьме, камере. Из уг … Словарь русского арго
квадрат — (Quad) 1. Одна из основных единиц типометрической системы Дидо, равная 4 цицеро, или 48 пунктам. 1 квадрат равен 18,048 мм. 2. Пробельный материал, используемый при изготовлении наборных печатных форм способа высокой печати. Квадраты различают по … Шрифтовая терминология
«Квадрат» — «Квадрат», клуб любителей джазовой музыки (джаз клуб). Создан в 1964 при ДК имени Ленсовета (с 1965 размещался в ДК имени С. М. Кирова, с 1986 во Дворце молодёжи). Объединяет музыкантов и любителей классического джаза. «Квадрат» продолжил… … Энциклопедический справочник «Санкт-Петербург»
КВАДРАТ — (от латинского quadratus четырехугольный), 1) равносторонний прямоугольник. 2) Вторая степень a2 числа a (название связано с тем, что именно так выражается площадь квадрата со стороной a) … Современная энциклопедия
Квадрат

Квадрат – прямоугольник с равными сторонами.
Квадрат – параллелограмм, у которого все стороны равны и все углы равны.
Свойства квадрата
Все свойства параллелограмма, ромба, прямоугольника верны для квадрата.
Признаки квадрата
Четырехугольник будет являться квадратом, если выполняется хотя бы одно из условий:
1. Все стороны равны и среди внутренних углов есть прямой угол.
2. Диагонали равны, перпендикулярны и, пересекаясь, делятся пополам.
3. Четырехугольник обладает поворотной симметрией: он не изменится при повороте на 90˚.
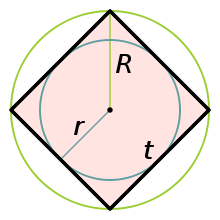
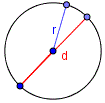
Описанная окружность
Около квадрата можно описать окружность. Сторона и радиус
окружности связаны соотношением:
Вписанная окружность
В квадрат можно вписать окружность. Радиус вписанной окружности и сторона квадрата связаны соотношением:
Площадь квадрата
Смотрите также таблицу-шпаргалку «Площади простейших фигур» здесь.
Чтобы не потерять страничку, вы можете сохранить ее у себя:
Геометрические фигуры. Квадрат.
Квадрат — правильный четырёхугольник. У квадрата все углы и стороны одинаковы.
Квадраты различаются лишь длиной стороны, а все 4 угла прямые и равны 90°.
Квадратом может стать параллелограмм, ромб либо прямоугольник, когда у них одинаковые длины диагоналей, сторон и равные углы.
Свойства квадрата.
— у всех 4-х сторон квадрата одинаковая длина, т.е. стороны квадрата равны:
— противолежащие стороны квадрата параллельны:
— каждый уг ол квадрата прямой:
— сумма углов квадрата равна 360°:
— каждая диагональ квадрата имеет такую же длину, как и другая:
— каждая из диагоналей квадрата делит квадрат на 2 одинаковые симметричные фигуры.
— угол пересечения диагоналей квадрата равен 90°, пересекая друг друга, диагонали делятся на две равные части:
AC┴BD;AO = BO = CO = DO = d/2
— точку пересечения диагоналей называют центр квадрата и она оказывается центром вписанной и описанной окружностей.
— все диагонали делят угол квадрата на две равные части, таким образом, они оказываются биссектрисами углов квадрата:
ΔABC = ΔADC = ΔBAD = ΔBCD
— диагонали делят квадрат на 4 одинаковых треугольника, кроме того, полученные треугольники в одно время и равнобедренные и прямоугольные:
ΔAOB = ΔBOC = ΔCOD = ΔDOA
Диагональ квадрата.
Диагональю квадрата является всякий отрезок, который соединяет 2-е вершины противолежащих углов квадрата.
Диагональ всякого квадрата больше стороны этого квадрата в √2 раз.
Формулы для определения длины диагонали квадрата:
1. Формула диагонали квадрата через сторону квадрата:
2. Формула диагонали квадрата через площадь квадрата:
3. Формула диагонали квадрата через периметр квадрата:
4. Сумма углов квадрата = 360°:
5. Диагонали квадрата одной длины:
6. Все диагонали квадрата делят квадрат на 2-е одинаковые фигуры, которые симметричны:
7. Угол пересечения диагоналей квадрата равен 90°, пересекая друг друга, диагонали делятся на две равные части:
8. Формула диагонали квадрата через длину отрезка l:
9. Формула диагонали квадрата через радиус вписанной окружности:
10. Формула диагонали квадрата через радиус описанной окружности:
R – радиус описанной окружности;
D – диаметр описанной окружности;
11. Формула диагонали квадрата через линию, которая выходит из угла на середину стороны квадрата:
C – линия, которая выходит из угла на середину стороны квадрата;
Вписанный круг в квадрат – это круг, примыкающий к серединам сторон квадрата и имеющий центр на пересечении диагоналей квадрата.
Площадь круга вписанного в квадрат меньше площади квадрата в π/4 раза.
Радиус окружности описанной вокруг квадрата больше радиуса вписанной окружности в √2 раз.
Радиус окружности описанной вокруг квадрата равен 1/2 диагонали.
Площадь круга описанного вокруг квадрата большая площадь того же квадрата в π/2 раз.
Основные геометрические фигуры
Основные понятия
Основные геометрические фигуры на плоскости — это точка и прямая линия. А простейшие фигуры — это луч, отрезок и ломаная линия.
Минимальный объект в геометрии — точка. Ее особенность в том, что она не имеет размеров: у нее нет высоты, длины, радиуса. У точки можно определить только ее расположение, которое принято обозначать одной заглавной буквой латинского алфавита.
Из множества точек может получится линия, а из нескольких соединенных между собой линий — геометрические фигуры.
Каждая математическая фигура имеет собственную величину, которую можно измерить при помощи формул и внимательности.
Площадь — это одна из характеристик замкнутой геометрической фигуры, которая дает нам информацию о ее размере. S (square) — знак площади.
Периметром принято называть длину всех сторон многоугольника. Периметр обозначается заглавной латинской P.
Если параметры переданы в разных единицах измерения длины, нужно перевести все данные к одной единице измерения.
Популярные единицы измерения площади:
Геометрические тела — часть пространства, которая ограничена замкнутой поверхностью своей наружной границы.
Если все точки фигуры принадлежат одной плоскости, значит она является плоской.
Объемная фигура — геометрическая фигура, у которой все точки не находятся на одной плоскости.
Примеры объемных геометрических фигур:
Рассмотрим подробнее некоторые фигуры, разберем их определения и свойства.
Прямоугольник
Прямоугольник — четырехугольник, у которого все стороны пересекаются под прямым углом.
Узнать площадь прямоугольника помогут следующие формулы:
Диагональ — это отрезок, который соединяет противоположные вершины фигуры. Он есть во всех фигурах, число вершин которых больше трех.
Периметр прямоугольника — сумма длины и ширины, умноженная на два.
P = 2 × (a + b), где a — ширина, b — высота.
Квадрат
Квадрат — это тот же прямоугольник, у которого все стороны равны.
Найти площадь квадрата легко:
Периметр квадрата — это длина стороны, умноженная на четыре.
P = 4 × a, где a — длина стороны.
Трапеция
Трапеция — это четырехугольник, у которого две стороны параллельны, а две не параллельны.
Основное свойство: в трапецию можно вписать окружность, если сумма ее оснований равна сумме боковых сторон.
Как найти площадь трапеции:
S = (a + b) : 2 × h, где a, b — два разных основания, h — высота трапеции.
Построить высоту трапеции можно, начертив отрезок так, чтобы он соединил параллельные стороны и был расположен перпендикулярно к этим основаниям.
Формула периметра для равнобедренной трапеции отличается от прямоугольника тем, что у равнобедренной трапеции есть две равные стороны.
P = a + b + 2 × c, где a, b — параллельные стороны, c — две длины одинаковых сторон.
Параллелограмм и ромб
Параллелограмм — четырехугольник, противоположные стороны которого попарно параллельны
Ромб — это параллелограмм с равными сторонами.
Общие формулы расчета площади фигур:
Периметр ромба — это произведение длины стороны на четыре.
P = 4 × a, где a — длина стороны.
Периметр параллелограмма — сумма длины и ширины, умноженная на два.
P = 2 × (a + b), где a — ширина, b — высота.
Треугольник
Треугольник — это такая фигура, которая образуется, когда три отрезка соединяют три точки, не лежащие на одной прямой. Эти три точки принято называть вершинами, а отрезки — сторонами.
Рассчитать площадь треугольника можно несколькими способами по исходным данным, давайте их рассмотрим.
S = 0,5 × a × h, где a — длина основания, h — высота, проведенная к основанию.
Основание может быть расположено иначе, например так:
При тупом угле высоту можно отразить на продолжение основания:
При прямом угле основанием и высотой будут его катеты:
S = 0,5 × a × b × sinα, где a и b — две стороны, sinα — синус угла между ними.
S = (a × b × с) : 4 × R, где a, b и с — стороны треугольника, а R — радиус описанной окружности.
S = p × r, где р — полупериметр треугольника, r — радиус вписанной окружности.
Периметр треугольника — это сумма длин трех его сторон.
P = a + b + c, где a, b, c — длина стороны.
Формула измерения периметра для равностороннего треугольника — это длины стороны, умноженная на три.
P = 3 × a, где a — длина стороны.
Круг — это множество точек на плоскости, которые удалены от центра на равном радиусу расстоянии.
Окружность — это граница круга.
Радиус окружности — это расстояние от центра окружности до любой точки на ней.
Диаметр круга — это отрезок, который соединяет две точки на окружности и проходящий через ее центр. Диаметр круга равен двум его радиусам.
Формулы площади круга:
Периметр круга или длина окружности — это произведение радиуса на два Пи или произведение диаметра на Пи.
L = d × π = 2 × r × π, где d — диаметр, r — радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.
Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)
Записаться на марафон
Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)
Что такое квадрат: определение и свойства
В данной публикации мы рассмотрим определение и свойства (с рисунками) одной из основных геометрических фигур – квадрата.
Определение квадрата
Свойства квадрата
Свойство 1
Диагонали квадрата равны, расположены под прямым углом друг к другу, в точке пересечения делятся пополам.
Свойство 2
Диагонали квадрата являются биссектрисами его углов. Для рисунке выше:
Свойство 3
Центром описанной вокруг и вписанной в квадрат окружностей является точка пересечения его диагоналей (в нашем случае – E).
При этом радиусы окружностей можно вычислить через длину стороны или диагонали квадрата:
Также, один радиус можно выразить через другой:
Свойство 4
Зная длину стороны или диагонали квадрата, можно найти его площадь или периметр.
Периметр (P) квадрата через сторону:
P = a + a + a + a = 4 ⋅ a
Периметр (P) квадрата через диагональ:
Площадь (S) квадрата через сторону:
Площадь (S) квадрата через диагональ:
| Квадрат | |
 | |
| Рёбра | |
|---|---|