как рассчитать давление на пол
Лабораторная работа «Определение давления, оказываемого человеком на пол» (учебный проект)
«Определение давления, оказываемого человеком на пол»
Цель: научиться определять давление, оказываемое телом на поверхность.
Приборы и материалы: весы, линейка, лист бумаги в клетку.
3. Вычислить давление по формуле: p = P / S
4. Результаты эксперимента занесите в таблицу:
Это результаты наших измерений:
Вывод: Давление, которое оказывает ученик 7 класса на пол равно 8837 Па.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс профессиональной переподготовки
Физика: теория и методика преподавания в образовательной организации
Курс повышения квалификации
Современные педтехнологии в деятельности учителя
Представлен проект лабораторной работы, разработанный обучающимися 7 класса на курсе «Проекты лабораторных работ по физике». Обучающиеся самостоятельно планируют выполнение работы, проводят измерения, оценивают результат, оформляют работу согласно требованиям. Потом представляют работу для защиты.
Темы проектов несложные, так как в 7 классе физику только начинают изучать.
Номер материала: ДБ-1347511
Международная дистанционная олимпиада Осень 2021
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
В школе в Пермском крае произошла стрельба
Время чтения: 1 минута
Минпросвещения намерено включить проверку иллюстраций в критерии экспертизы учебников
Время чтения: 1 минута
Школьников не планируют переводить на удаленку после каникул
Время чтения: 1 минута
ВШЭ перейдет на удаленку до конца года
Время чтения: 1 минута
Студенты разработали программу для предупреждения опасного поведения в школах
Время чтения: 1 минута
Минпросвещения разрешило школам вводить каникулы до 30 октября
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Для чего и как рассчитывается нагрузка на перекрытие жилого дома кг/м2?

Плиты укладываются в пролёте между вертикальными опорами – стенами, пилонами или колоннами.
Преимущественно работают на изгиб и выполняют роль жёсткого диска, объединяющего отдельные элементы каркаса сооружения в единую геометрически неизменяемую систему.
При расчёте плит перекрытий определяются такие важные параметры, как их толщина, армирование, прогиб и необходимость устройства дополнительных подпирающих элементов (балок или капителей).
Как провести расчет нагрузок на перекрытие, расскажем далее.
Что это такое?
Нагрузки, прикладываемые к перекрытию, представляют собой сочетание внешних сил, действующих на конструктивный элемент, вызывая в нём внутренние усилия. Несущая способность элемента определяется из условия равновесия, достигаемого при приложении нагрузок.
Виды нагрузок на плиты перекрытий по СНиП и СП
Нагрузки на пролётные конструкции определяются, исходя из требований нормативных документов – СНиП 2.01.07-85 и его обновлённой версии – СП 20.13330.2011 «Нагрузки и воздействия».
В соответствии с пунктами этих нормативов, нагрузки классифицируются на следующие виды:
Например, в жилых квартирах или частных домах – это нагрузки от мебели, бытовых приборов и самих жильцов.
В зависимости от функционального назначения помещений, величины полезных нагрузок различаются.
Расчёт пролетных конструкций
Расчёт пролётных конструкций ведётся по двум группам предельных состояний:
На несущую способность плит перекрытий влияет величины постоянных и полезных нагрузок, толщина элемента, длина пролёта и условия эксплуатации помещения.
Как рассчитать значения?
Расчёт нагрузок на плиту перекрытия производится методом суммирования всех приложенных к конструктивному элементу внешних сил, с учётом различных коэффициентов запаса, принимаемых по указанному выше СНиП. Если рассмотреть теоретические выкладки, то расчёт нагрузок делится на следующие категории:
Предельные

Например, на основании представленного ниже расчёта – при приложении суммарной расчётной нагрузки 900 кг/м 2 на плиту перекрытия толщиной 200 мм, армированную прутками d10 A500s с шагом 200 мм, достигается фактический изгибающий момент М = 2812,5 кН*см при пролёте 5 м.
А сечение с такими параметрами остаётся в равновесии при достижении момента Мпред = 2988.5 кН*см, что всего на 5,8% выше предельного значения.
Точечные
Как правило, такие силы не прикладываются к перекрытию отдельно – всегда существуют постоянные нагрузки, и единичное точечное загружение суммируется с ними.
Приложенная точечная нагрузка влияет на значение опорных реакций и величину изгибающего момента в расчётном сечении. Усилия от точечного загружения определяется как произведение силы на плечо (расстояние от ближайшей точки опоры).
Например, если в комнате с пролётом 5 метров стоит декоративная колонна массой 500 кг на расстоянии от стены 2 м, то расчётная нагрузка с учётом коэффициента запаса (gn для постоянных сил = 1,05) составит 525 кг. Момент в данной точке составит 525 кг х 2 м = 1050 кг * м, или 1050 кН * см.
Соответственно, при добавлении равномерно распределённого загружения, описанного выше, стандартное сечение плиты с армированием d10 A500s с шагом 200 мм не будет удовлетворять расчёту прочности, и данное место следует усилить дополнительными стержнями, например, d10 A500s ш. 200 + d12 A500s ш. 200.
Пересчёт на м 2

СНиП допускает не производить расчёт временных нагрузок на плиту от конкретных предметов, а учитывать приведённую равномерно-распределённую по площади поверхности силу.
Например, вдоль стены комнаты, на протяжении 3 м стоит гарнитур общей массой 400 кг, напротив – диван массой 200 кг и другие предметы мебели с разными весами. По данному помещению каждый день передвигаются 4 человека с массами тела от 50 до 120 кг.
Пример
Ниже представлен пример сбора нагрузок на перекрытие в частном жилом доме. По условию задачи, габариты комнаты составляют 7 х 4 м, плита перекрытия 200 мм, поверх которой уложена ц/п стяжка толщиной 50 мм по подложке из экструдированного пенополистирола 30 мм, а в качестве чистового пола применяется керамогранитная плитка толщиной 12 мм с клеевым составом 3 мм.
Требуется собрать расчётные нагрузки на данную конструкцию для последующего расчёта. Задача решается с выполнением следующих этапов:
Собственный вес плиты – M1 = S x h x rбет, где:
Масса полов – M2 = mподл + mстяж + mплит, где:
M2 = 24 кг + 1800 кг + 720 кг = 2544 кг. В жилом помещении рекомендуемая по СНиП временная нагрузка составляет q = 150 кгс/м2.
Таким образом, суммарная полезная нагрузка на плиту составляет F = q x S = 150 х 20 = 3000 кг:
Таким образом, Fобщ расч = (M1 + M2) x gnс пост + F x gn врем = (10000 кг + 2544 кг) х 1,1 + 3000 кг х 1,4 = 13798,4 кг + 4200 кг = 17998.4 кг
18000 кг, или 1800 кН.
При наличии точечной или штамповой нагрузки от веса какого-либо оборудования, она участвует в расчёте отдельно, формируя линейную, а не квадратичную зависимость изгибающего момента.
В отдельных случаях допускается разложить точечную нагрузку на равномерно распределённую по площади, с учётом повышающего коэффициента, так как железобетон не является упругим материалом, и все усилия в нём перераспределяются в большей части его объёма.
Изгибающий момент
Безбалочная плита перекрытия должна удовлетворять расчёту по прочности, или первой группе предельных состояний. Чтобы определить несущую способность перекрытия, необходимо выполнить следующий алгоритм:
Если данные показатель меньше 2, то плита считается опёртой по контуру, и расчёт ведётся относительно того пролёта, в котором возникает наибольший изгибающий момент.
В рассматриваемом примере балка имеет сечение b x h = 1 м х 0,2 м, и к ней приложена нагрузка qрасч = 900 кг/м, или 90 кН/м.
Величина изгибаемого момента для подобной конструкции составляет M = qрасч х l 2 / 8, где l – величина пролёта, или 5 м. M = 90 кН/м х 5 х 5 / 8 = 281.25 кН*м, или 2812,5 кН*см.
Величина изгибающего момента может быть отображена на эпюре данного вида усилия, возникающего в конструкции.
Как посчитать несущую способность?
При известной величине изгибающего момента и габаритов (жёсткости сечения) можно определить несущую способность данного пролётного элемента по следующим формулам:
Высота сечения плиты складывается из двух величин h = h0 + a, где h0 – рабочая высота от нижней арматуры, находящейся в зоне растяжения до верхней грани бетона. а – величина защитного слоя бетона. Как правило, этот показатель в тонких плитах варьируется в пределах от 15 до 25 мм. h0 = h – a = 200 мм – 20 мм = 180 мм.
В строительной механике, согласно по СП 63.13330.2018 «Бетонные и железобетонные конструкции», существуют два условия, при которых конструкция достигает предельного равновесия под действием внешних сил.
В условии равновесия х – абсолютная величина сжатой зона бетона, которая равняется х = Rs Аs / gb1 Rbb (по СП 63.13330.2018 «Бетонные и железобетонные конструкции»):
Требуемая площадь рабочей арматуры зависит от расчётных параметров сечения и величины внутренних усилий (в плите перекрытия – изгибающего момента).
Для предотвращения образования трещин от усадки бетона, в плитах перекрытий шаг рабочей арматуры, чаще всего, назначается 200 мм. Таким образом, в расчётной полосе шириной 1 м располагается 5 рабочих стержней.
На завершающем этапе из основного условия равновесия определяется предельно допустимый момент, который может возникнуть в сечении плиты перекрытия. M = gb1 Rbbx(h0 – x/2) = 0,9 х 1,7 х 100 х 1,12 х (18 – 1,12/2) = 2988.5 кН*см.
Далее остаётся сравнить предельно допустимый момент 2988.5 кН*см с фактическим усилием, возникающим после приложения нагрузок – 2812,5 кН*см, который оказался меньше, значит, условие прочности выполняется.
В случае, если условие предельного равновесия не достигается, толщина плиты, а также расчётное количество рабочей арматуры должны быть пересмотрены.
Прочность ЖБ элемента
В строительной механике понятия прочности и несущей способности практически не имеют различий. Однако, на практике это не совсем так. Прочность – это способность конструктивного элемента не разрушаться под действием внешних сил. Несущая способность – это способность конструктивного элемента удовлетворять предъявленным к нему эксплуатационным требованиям под действием сочетания нагрузок.
Таким образом, расчёт по предельным состояниям 1 группы, приведённый выше, показывает, что плита перекрытия остаётся в статическом положении не разрушается, (то есть, обеспечивается её прочность) и может эксплуатироваться в нормальных условиях (так как в расчёте были учтены все коэффициенты условий работы). Проведения дополнительных прочностных расчётов не требуется.
Возможные сложности и ошибки
При расчёте сечения плиты перекрытия на прочность, следует учитывать важные нюансы, чтобы не допустить серьёзных ошибок:
Последствия неверных расчётов могут привести к обрушению строительных конструкций, недопустимым прогибам и другим непоправимым проблемам во время эксплуатации сооружения.
Заключение
Перед назначением толщины и армирования плиты перекрытия необходимо провести расчёт прочности изгибаемого элемента. Вычисления выполняются после сбора постоянных и временных нагрузок и определения внутренних усилий в конструкции.
Если результаты расчёта не удовлетворяют условиям предельного равновесия, необходимо задать другую толщину плиты и провести вычисления заново.
Как правильно рассчитать нагрузки на полы?
Проектирование – это крайне ответственный этап строительства здания или конструкции. Именно на этом этапе определяется надежность структурных элементов и их долговечность. Ошибки при проектировании могут стать причиной появления критических дефектов и не позволить нормально эксплуатировать объект. В полной мере это относится и к проектированию бетонных полов.
К сожалению, многие проектировщики ошибочно не выделяют полы в особый вид конструкций и применяют к ним те же подходы, что и к фундаментам или другим бетонным элементам. В результате бетонная плита пола может быть запроектирована, как с избыточным запасом прочности (то есть может быть неоправданно дорогой и материалоемкой), так и наоборот – недостаточно надежной. И хотя полы не относятся к разряду ответственных конструкций, их прочностные характеристики важны для безопасной и эффективной эксплуатации объекта строительства в будущем.
Особенно важным в этой связи является определение воздействий и нагрузок, которым будет подвергаться бетонный пол. Характер воздействий, в первую очередь, повлияет на выбор покрытия пола, и этот вопрос заслуживает отдельного рассмотрения. Однако и с определением нагрузок возникает ряд спорных моментов, причем трудности зачастую возникают даже у опытных проектировщиков.
Равномерно распределенная нагрузка
Тем не менее, нередко приходится сталкиваться со случаями, когда нагрузки в виде МПа/м2 указываются для склада со стеллажным хранением. Налицо неверный подход, при котором инженер делит сумму всех складских или производственных нагрузок на площадь. Иногда встречаются случаи, когда берется несущая способность стеллажа и делится на площадь, которую он занимает. Расчеты, выполненные на таких исходных данных, скорее всего, будут в корне неверными.
Сосредоточенная нагрузка
Дело в том, что в случае стеллажного складирования имеет место не распределенная нагрузка, а сосредоточенная (или точечная). Товары размещаются на многоярусных стеллажах, которые в свою очередь имеют небольшую площадь опирания на полы. Это создает очень серьезные нагрузки на плиты полов.
Как правильно посчитать сосредоточенную нагрузку?
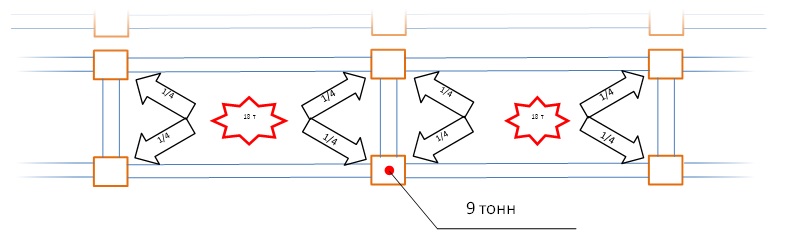
За значение сосредоточенной нагрузки принимается давление под сдвоенной пяткой стеллажа. Сдвоенная опора находится между секциями стеллажа, и на нее приходится вдвое большая нагрузка, нежели на торцевые опоры. Для правильного расчета нагрузки нужно взять суммарную номинальную вместимость всех ярусов стеллажа, кроме напольного, и разделить на два. Рассмотрим пример: имеется стеллаж с пятью ярусами (напольный ярус не учитывается), на каждом из которых может храниться 3 паллета массой 1.200 кг:
5 х 3 х 1,2 = 18 тонн
То есть на каждой секции хранится до 18 тонн груза.
Этот вес распределяется между четырьмя опорами, однако на опоры между секциями приходят нагрузки сразу с двух сторон. Таким образом, нагрузка на каждую опору составит 9 тонн (см. иллюстрацию).
При передаче данных инженеру-проектировщику следует также указать размер пятки опоры стеллажа, поскольку пятка размерами 110х110 мм создает при равной нагрузке почти вдвое большее давление на полы, чем пятка 150х150 мм.
Также большое влияние имеет расстояние между смежными рядами стеллажей.
Такой же подход к определению нагрузок используют и применительно к производственному оборудованию, если оно устанавливается непосредственно на полы. Вес станков и производственных линий распределен между стойками и опорами, поэтому представляет собой сосредоточенную нагрузку.
В случаях высотного складирования нагрузки на одну опору могут достигать 10-12 тонн. В таких ситуациях допускается использование понижающего коэффициента, учитывающего степень заполняемости склада.
Другие виды нагрузок
Также в целях проектирования принято выделять и другие виды нагрузок на полы.
Колесная нагрузка – создается транспортными средствами, заезжающими на полы и перемещающимися по ним. Для правильной спецификации этих нагрузок необходимо знать распределение веса между осями транспортного средства и размер пятна контакта колеса с поверхностью. Также важно знать, парные ли колеса, какое расстояние между ними во всех направлениях. Хотя этот тип нагрузок схож с точечными, они обладают отличительной особенностью – динамикой. То есть при движении происходит приращение воздействующей на полы силы, что должно найти свое отражение в проектных расчетах.
Линейная нагрузка
Отдельные виды систем хранения грузов имеют вытянутые и узкие опоры, что позволяет рассматривать их как линейную нагрузку. В техническом задании на проектирование необходимо указать геометрические параметры этих опор, расстояния между ними и, естественно, массу складируемых на них товаров или материалов. Находящиеся непосредственно на полу рельсы тоже создают этот тип нагрузки, и к ним применяются те же подходы.
Специфика нагрузок, имеющих место на предприятии, неотделима от понимания технологических процессов и характеристик используемого оборудования. Если Вы испытываете трудности с описанием нагрузок на Вашем объекте, Вы можете обратиться в компанию «Би Райт» за консультацией, и наши специалисты по проектированию полов помогут Вам.
Закон Паскаля
Давление
Идущий по рыхлому снегу человек будет в него постоянно проваливаться. А вот на лыжах он сможет передвигаться по тому же самому снегу спокойно. Казалось бы, ничего не меняется — человек воздействует на снег с одинаковой силой и на лыжах, и без них.
Дело в том, что «проваливание» в снег характеризуется не только силой — оно также зависит от площади, на которую эта сила воздействует. Площадь поверхности лыжи в 20 раз больше площади поверхности подошвы, поэтому человек, стоя на лыжах, действует на каждый квадратный сантиметр с силой в 20 раз меньшей, чем без них.
Или, например, если вы будете с одинаковой силой втыкать кнопки в пробковую доску, легче войдет та кнопка, у которой более заостренный конец, так как его площадь меньше.
Резюмируем: результат действия силы зависит не только от ее модуля, направления и точки приложения, но и от площади поверхности, к которой эта сила приложена.
А теперь подтвердим этот вывод опытами, как настоящие физики.
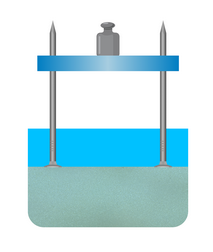
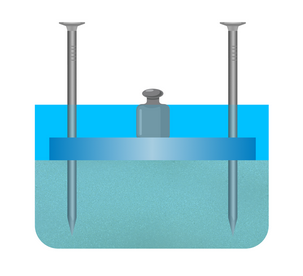
Возьмем небольшую доску и вобьем гвозди в ее углы. Также возьмем емкость с песком и поставим конструкцию из доски и гвоздей в эту емкость. Сначала расположим конструкцию шляпками вниз и поставим на нее гирю. Конструкция не утонет в песке, а только чуть-чуть углубится в него.
Затем перевернем конструкцию так, чтобы шляпки гвоздей оказались сверху и также поставим на доску гирю. Теперь конструкция утонет в песке.
От того, какая сила действует на каждую единицу площади поверхности, зависит результат действия силы.
Во всех примерах мы говорили о действии силы, перпендикулярной поверхности. Чтобы охарактеризовать это действие, используется величина давление.
Давление
p = F/S
p — давление [Па]
F — сила [Н]
S — площадь [м 2 ]
Как уменьшить или увеличить давление
Тяжелый гусеничный трактор производит давление на почву, равное 40–50 кПа. Мальчик массой 45 кг производит давление всего лишь в 3 раза меньше, чем такой трактор. Это связано с большой площадью гусениц трактора.
В зависимости от того, какое давление хотят получить, площадь опор уменьшают или увеличивают. Например, чтобы уменьшить давление здания на грунт, в процессе строительства увеличивают площадь нижней части фундамента.
Шины грузовых автомобилей делают значительно шире легковых автомобилей. Чтобы убедиться в этом, обратите внимание на колеса какой-нибудь большой фуры. Самые широкие шины можно увидеть на автомобилях, предназначенных для передвижения в пустыне. Тот же лайфхак используется в шасси самолетов.
Обратную зависимость тоже применяют, например, при создании лезвий колющих и режущих инструментов. Острое лезвие имеет малую площадь, поэтому даже при небольшом нажатии создается большое давление.
Задачка раз
Книга лежит на столе. Масса книги равна 0,6 кг. Площадь ее соприкосновения со столом равна 0,08 м2. Определите давление книги на стол.
Решение
На стол будет давить сила, равная весу книги. Так как она покоится, ее вес будет равен силе тяжести. Следовательно:
p = mg/S = 0,6 × 10 / 0,08 = 75 Па
Ответ: давление книги на стол будет равно 75 Па.
Задачка два
Решение:
p = mg/S = 6 610 × 10 / 1,4 = 47 214 Па = 47,2 кПа
Ответ: давление трактора на почву составляет 47,2 кПа.
Задачка три
Человек массой 80 кг с сумкой весом 100 Н стоит неподвижно на полу. Сила давления подошв его ботинок на пол равномерно распределена по площади 600 см2. Какое давление человек оказывает на пол?
Решение
Масса человека: m = 80 кг.
Вес сумки, которую держит человек: Pc = 100 Н.
600 см 2 = 600 / 10 000 м 2 = 0,06 м 2
Давление — это отношение силы к площади, на которую она действует. В данном случае на площадь действует сила, равная сумме силы тяжести человека и веса сумки:
Поэтому давление, оказываемое человеком с сумкой на пол, равно:
p = (mg + Pс) / S = (80 × 10 + 100) / 0,06 = 15 000 Па = 15 кПа
Ответ: давление человека с сумкой на пол равно 15 кПа.
Определение закона Паскаля
Итак, мы подошли к формулировке закона Паскаля, и звучит она так:
Давление, производимое на жидкость или газ, передается в любую точку одинаково во всех направлениях.
Обратите внимание — закон работает только с жидкостями и газами. Дело в том, что молекулы жидких и газообразных веществ под давлением ведут себя совсем не так, как молекулы твердых тел. Если молекулы жидкости и газа движутся почти свободно, то молекулы твердых тел так не умеют. Они могут лишь колебаться, немного отклоняясь от исходного положения. Именно благодаря свободному передвижению молекулы газа и жидкости оказывают давление во всех направлениях.
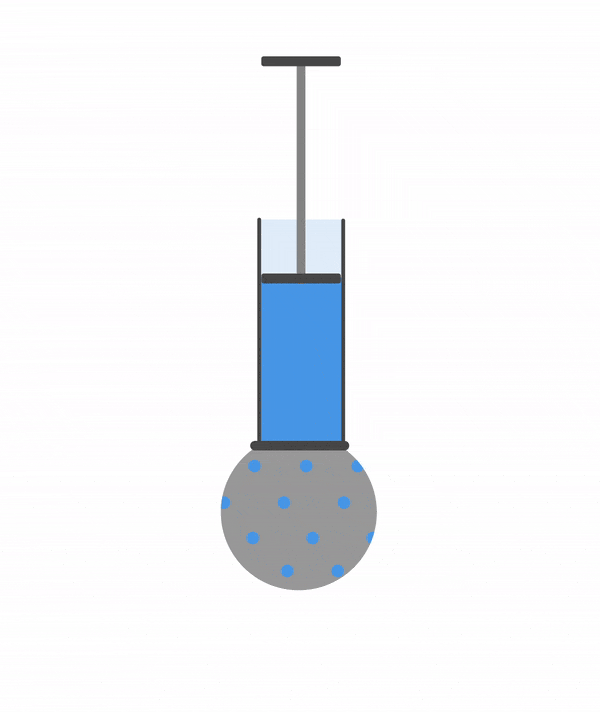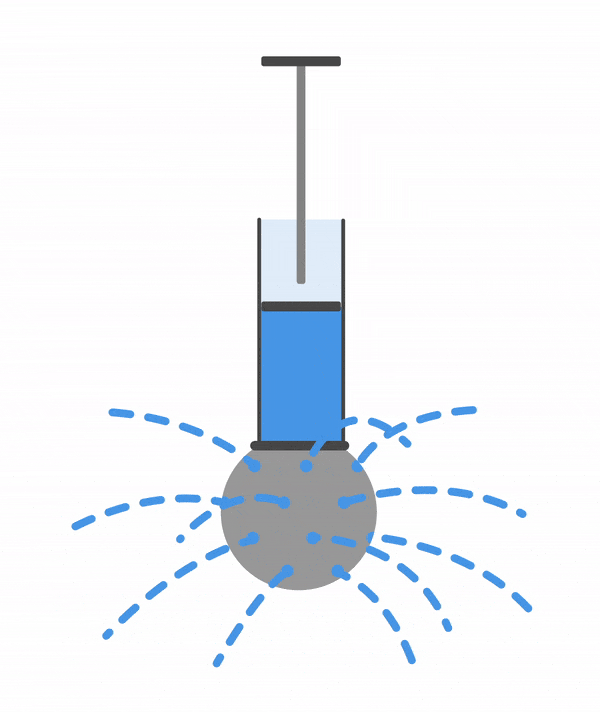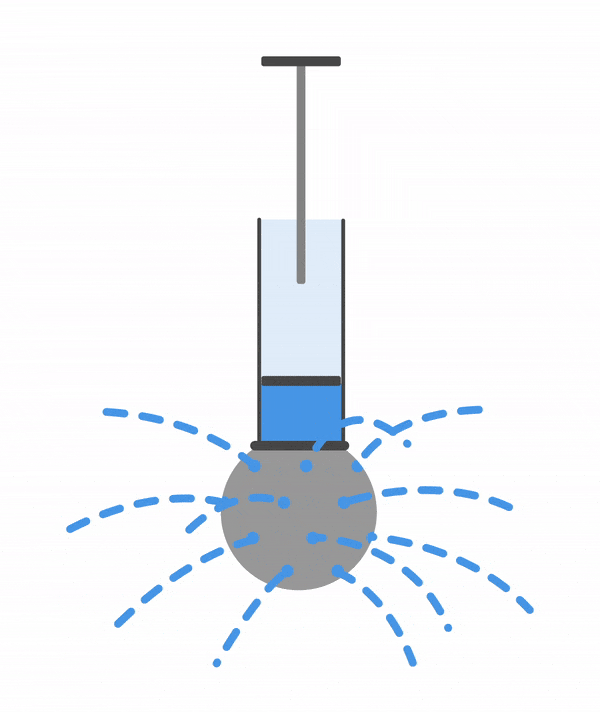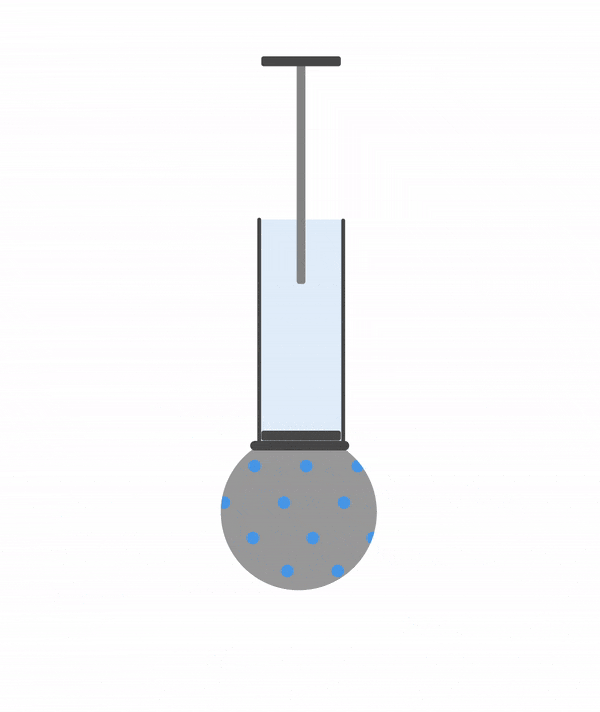
Рассмотрим опыт с шаром Паскаля, чтобы стало понятнее.
Присоединим к трубе с поршнем полый шар со множеством небольших отверстий. Зальем в шар воду и будем давить на поршень. Давление в трубе вырастет и вода будет выливаться через отверстия, причем напор всех струй будет одинаковым. Такой же результат получится, если вместо воды в шарике будет газ.
Давление жидкости
Из закона Паскаля следует, что раз давление передается одинаково во всех направлениях, то верхние слои жидкости давят на средние, средние — на нижние, нижние — на дно сосуда.
Давление внутри жидкости на одном и том же уровне одинаково по всем направлениям. С глубиной давление увеличивается.
Это утверждение проверяется с помощью манометра — прибора для измерения давления. Чем глубже мы измеряем давление, тем больше показания.
Давление столба жидкости
p = ρgh
ρ — плотность [кг/м 3 ]
h — высота столба жидкости [м]
g — ускорение свободного падения [м/с 2 ]
На Земле g = 9,8 м/с 2
Формула давления столба жидкости часто требуется в задачах.
Задачка раз
На горизонтальном столе стоят два цилиндрических сосуда — узкий и широкий (см. рисунок). В узкий сосуд налита вода, в широкий — керосин. Уровень жидкости в сосудах одинаковый. Сравните давления p жидкостей в точках A, B, C, D и выберите правильную пару утверждений.
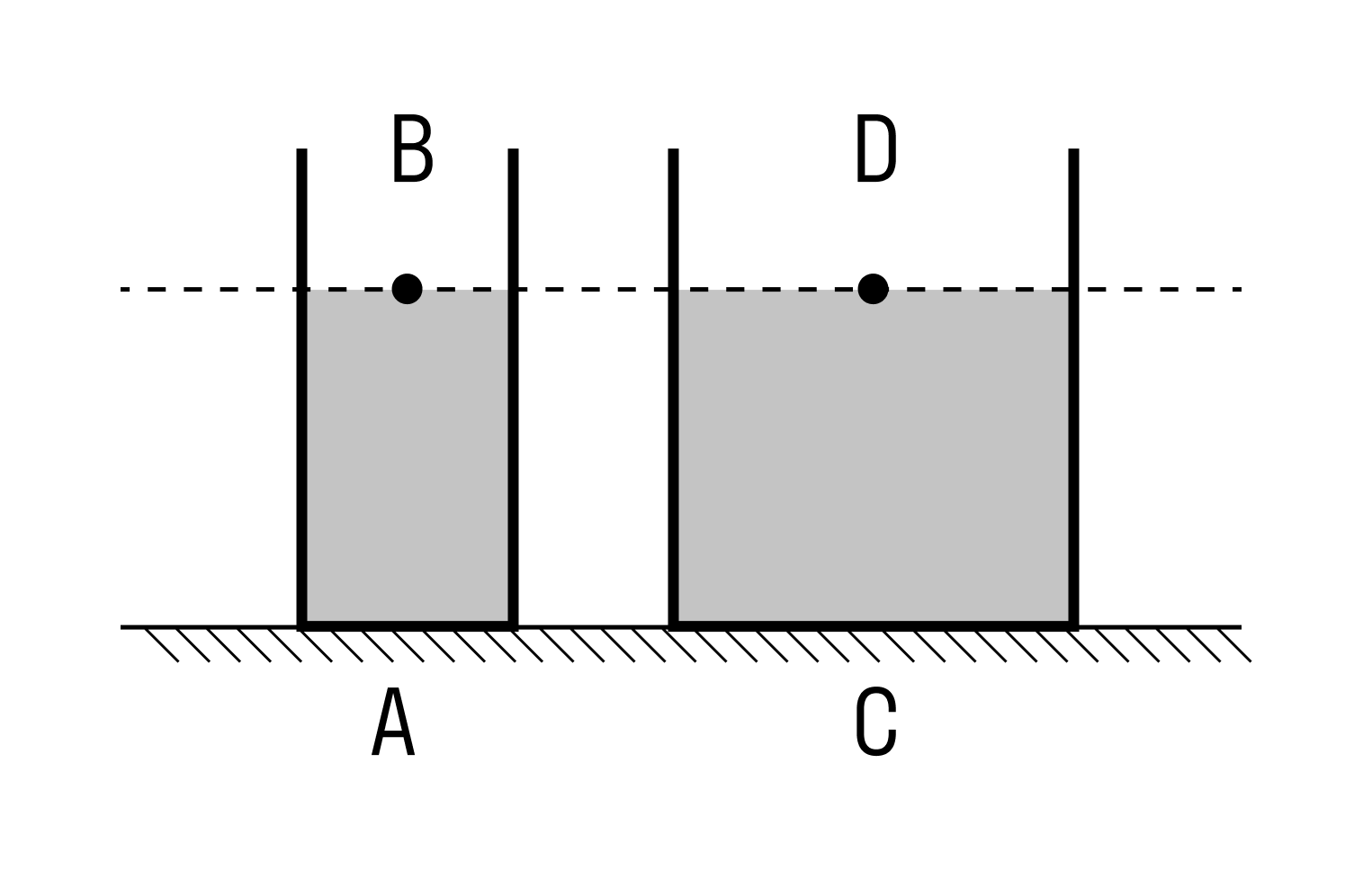
Решение
Давление столба жидкости прямо пропорционально ее плотности и высоте столба. Плотность воды больше плотности керосина, следовательно, давление в точке A больше давления в точке C. Давления в точках B и D равны.
Правильный ответ указан под номером 4.
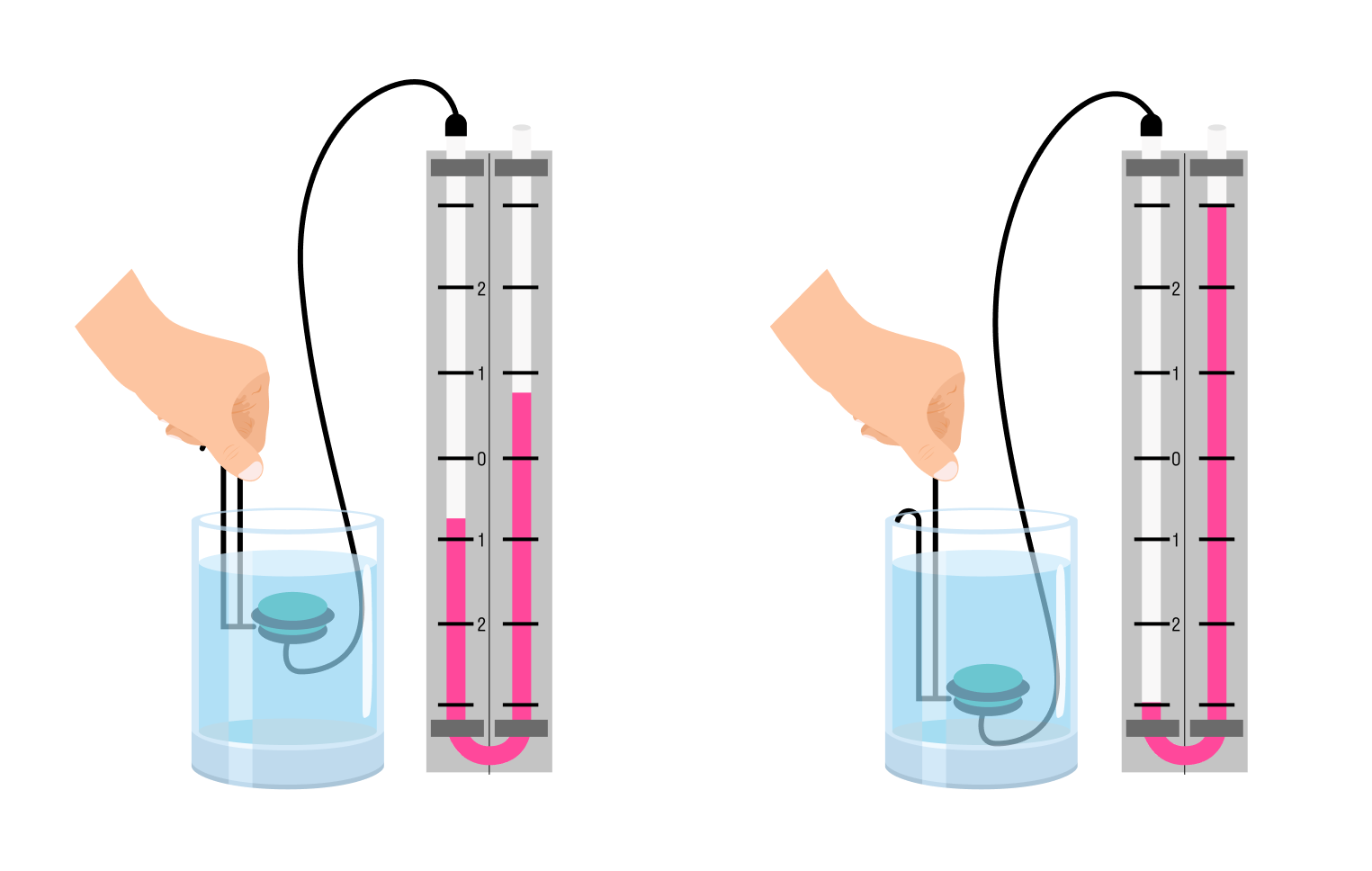
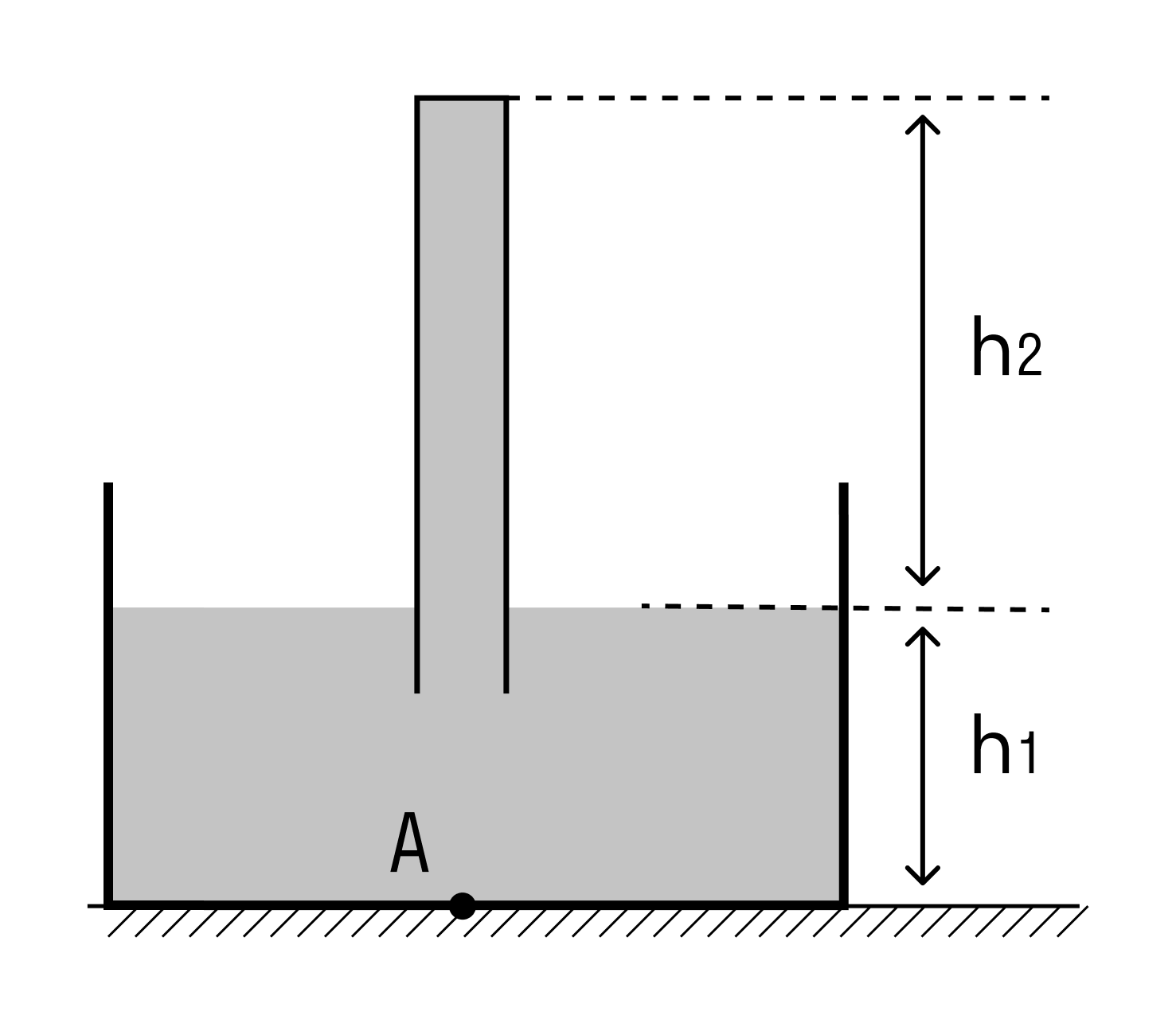
Задачка два
Решение
Поскольку вода не вытекает из пробирки, давление столба высотой h2 на жидкость в сосуде высотой h1 уравновешено давлением, которое оказывает вода в сосуде на столб воды в пробирке. Сосуд открытый, поэтому на него действует внешнее давление, которое и передается столбу воды. В результате столб воды в пробирке не оказывает дополнительного давления на точку А, поэтому давление, оказываемое водой на дно сосуда в точке А, равно p = ρgh1. Тогда:
p = ρgh1 = 998 × 10 × 0,3 = 2 994 Па