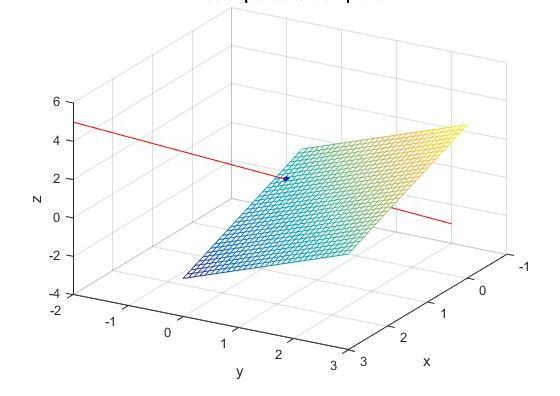
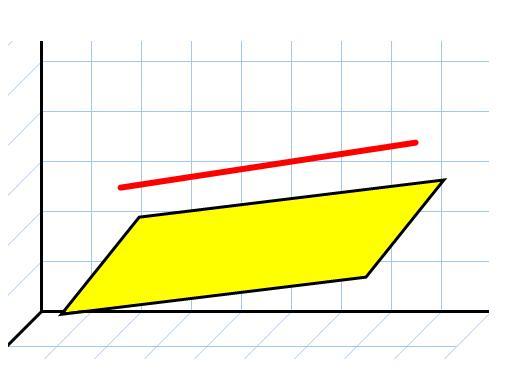
Говоря о взаимном расположении прямых и плоскостей в пространстве можно утверждать что
Взаимное расположение точки, прямых и плоскостей с примерами
Содержание:
Взаимное расположение точки и прямой:
Возможны два варианта расположения точки относительно прямой:
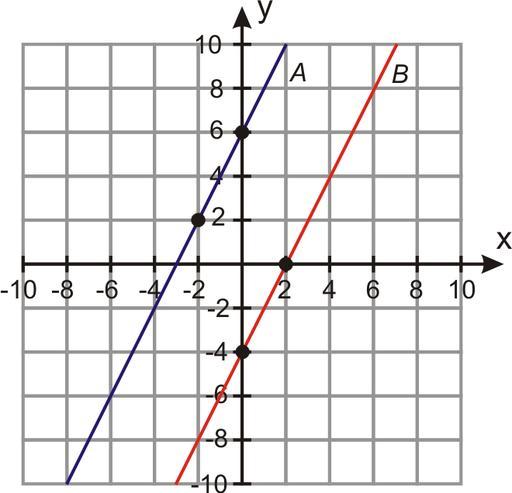
Взаимное расположение прямых
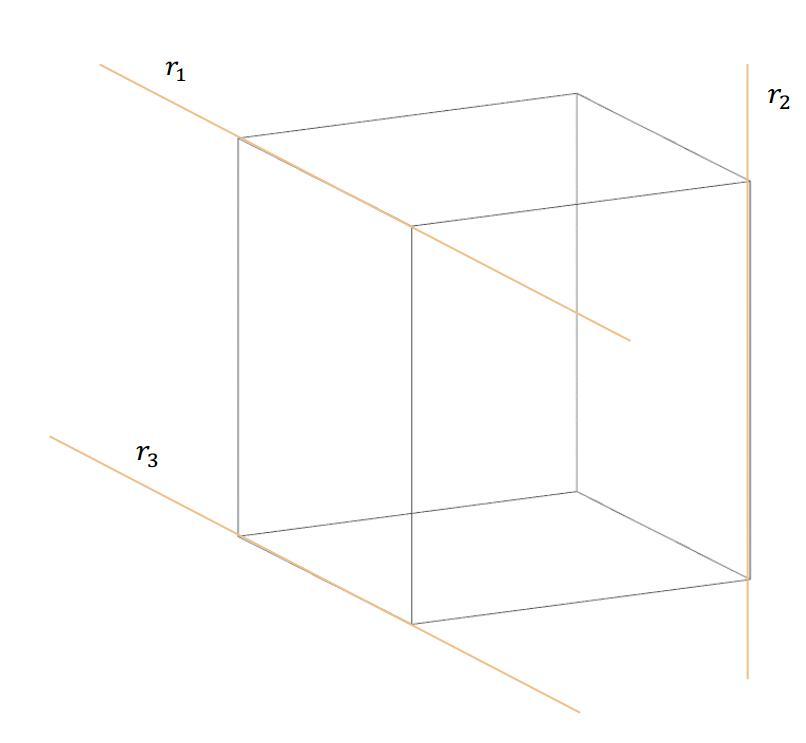
Прямые в пространстве могут занимать друг к другу одно из трех положений:
Параллельными называются прямые, лежащие в одной плоскости и не имеющие общих точек.
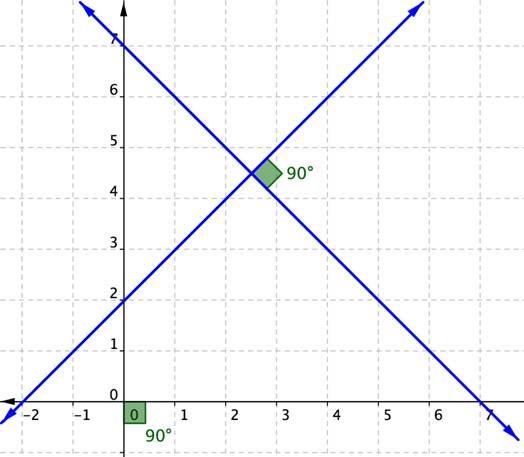
Пересекающимися называются прямые, лежащие в одной плоскости и имеющие одну общую точку.
У пересекающихся прямых на КЧ одноименные проекции пересекаются в проекциях точки А. Причем фронтальная 
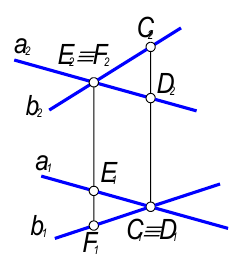
Скрещивающимися называются прямые, лежащие в параллельных плоскостях и не имеющие общих точек.
Если прямые скрещивающиеся, то на КЧ их одноименные проекции могут пересекаться, но точки пересечений одноименных проекций не будут лежать на одной линии связи.
На рис. 3.4 точка С принадлежит прямой b, а точка D на прямой а. Эти точки находятся на одинаковом расстоянии от фронтальной плоскости проекций.
Плоскость. Способы ее задания, положение относительно плоскостей проекций
Положение плоскости в пространстве может быть однозначно определено:
Всегда от одного способа задания плоскостей можно перейти к другому.
След плоскости – это линия пересечения заданной плоскости с одной из плоскостей проекций.
Соответственно различают горизонтальный, фронтальный и профильный следы плоскости.
Плоскостью общего положения называется плоскость не параллельная и не перпендикулярная ни одной из плоскостей проекций.
Плоскостями частного положения относительно плоскостей проекций называются плоскости параллельные или перпендикулярные им.
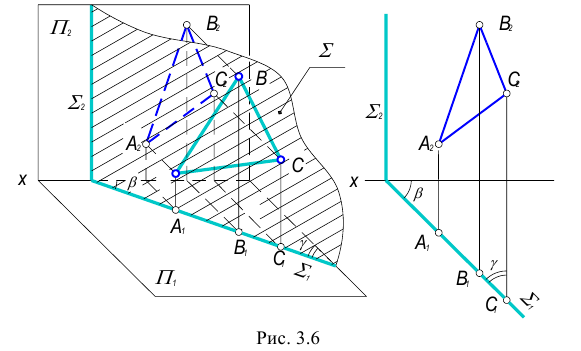
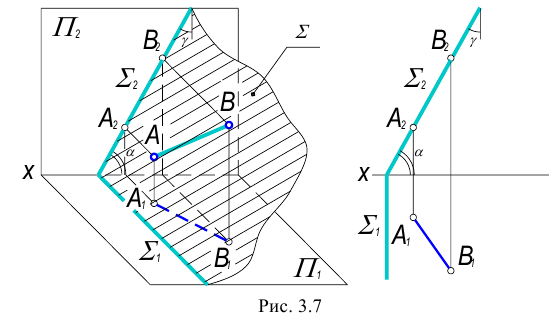
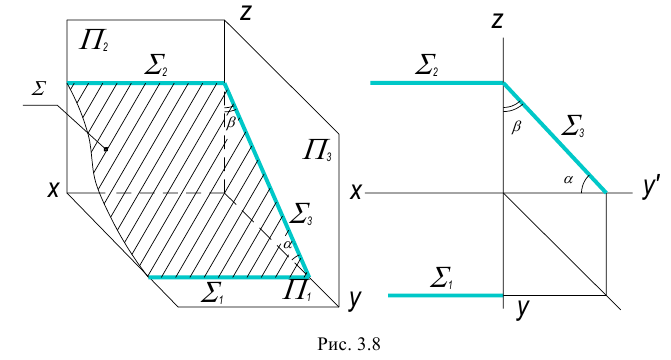
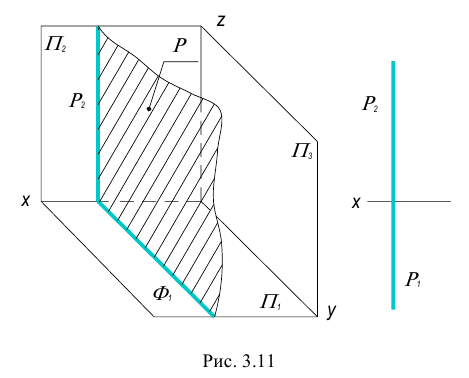
Плоскость перпендикулярная одной из плоскостей проекций называется проецирующей плоскостью.
Существует три вида проецирующих плоскостей: горизонтально- проецирующая, фронтально-проецирующая и профильно-проецирующая плоскости. Такие плоскости вырождаются в прямую линию (след плоскости) на ту плоскость проекций, к которой они перпендикулярны.
2. Фронтально-проецирующая плоскость – плоскость перпендикулярная фронтальной плоскости проекций.
3. Профильно-проецирующая плоскость – плоскость, перпендикулярная профильной плоскости проекций.
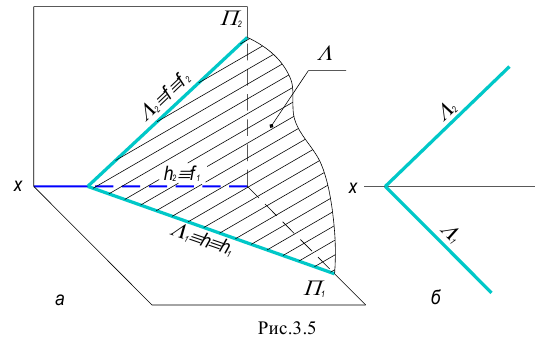
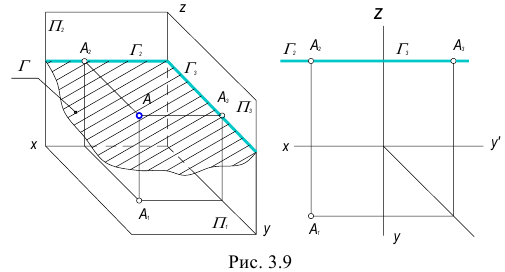
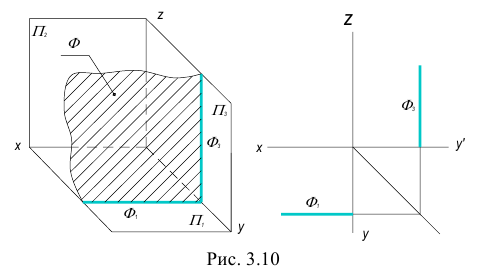
Плоскость, параллельная одной из плоскостей проекций, называется плоскостью уровня.
Существует три вида плоскостей уровня: горизонтальная, фронтальная и профильная плоскости уровня.
1. Горизонтальная плоскость – плоскость, параллельная горизонтальной плоскости проекций.
3. Профильная плоскость – плоскость, параллельная профильной плоскости проекций.
Принадлежность прямой и точки плоскости
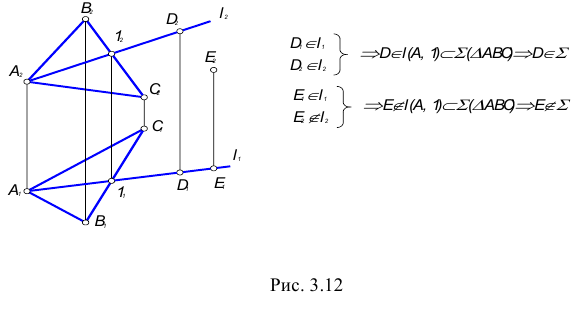
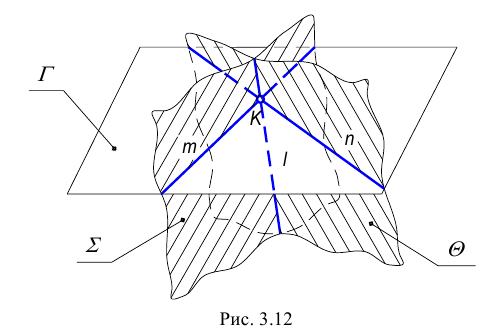
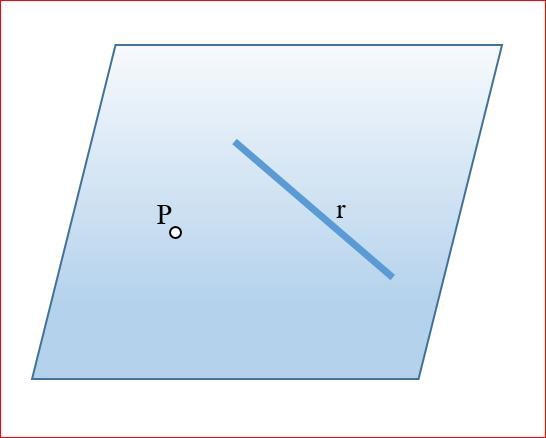
Возможны два случая расположения точки относительно плоскости: точка может принадлежать плоскости или не принадлежать ей (рис. 3.12).
Точка принадлежит плоскости, если принадлежит прямой, лежащей в этой плоскости.
Прямая принадлежит плоскости, если имеет с ней две общие точки или имеет с ней одну общую точку и параллельна другой прямой, лежащей в этой плоскости.
На рис. 3.12 изображена плоскость 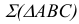
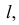
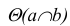
Взаимное расположение прямой и плоскости
Для прямой и плоскости возможны три случая их взаимного расположения:
Параллельность прямой и плоскости
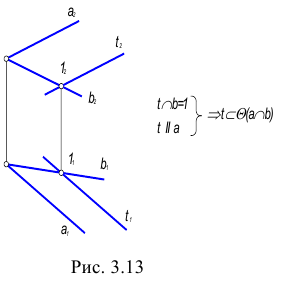
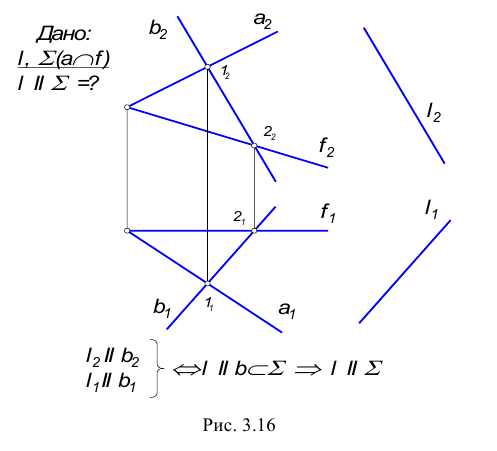
Прямая параллельна плоскости, если она параллельна прямой, принадлежащей этой плоскости.
Этот признак параллельности прямой и плоскости хорошо известен из курса стереометрии.
Взаимное расположение плоскостей
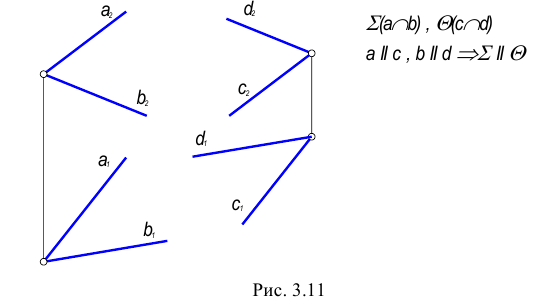
Плоскости по отношению друг к другу могут занимать два положения: быть параллельными или пересекаться.
Плоскости параллельны, если пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым второй плоскости
Если две плоскости не параллельны, то они обязательно пересекаются и результатом их пересечения является прямая.
Для построения линии пересечения плоскостей необходимо найти две точки, одновременно принадлежащие этим плоскостям, или одну общую точку, если известно направление линии пересечения.
Направление линии пересечения известно в том случае, если:
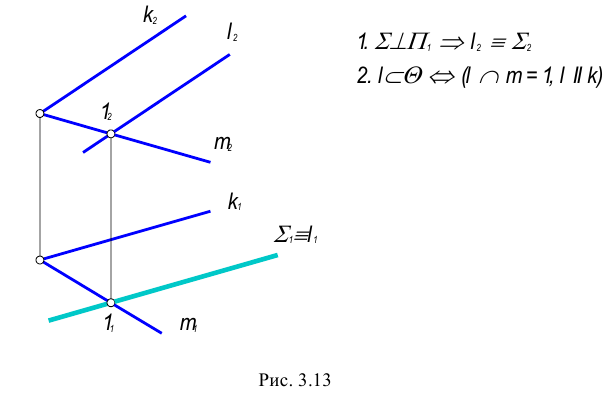
Общая точка для двух пересекающихся плоскостей в общем случае определяется с помощью вспомогательной плоскости частного положения, также пересекающей заданные плоскости по прямой (рис. 3.12).
Рассмотрим сначала частные случаи пересечение двух плоскостей:
1. Пересекаются плоскость общего положения 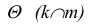
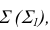
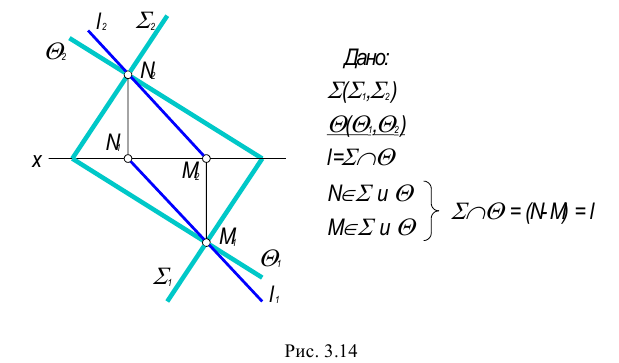
2. Пересекаются плоскости общего положения заданные следами.
В этом случае следы плоскости пересекаются в пределах чертежа, следовательно, линия пересечения этих плоскостей строится по двум точкам, являющимся следами линии пересечения, которые находятся в точках пересечения одноименных следов плоскостей.
Рассмотрим общий случай пересечения плоскостей:
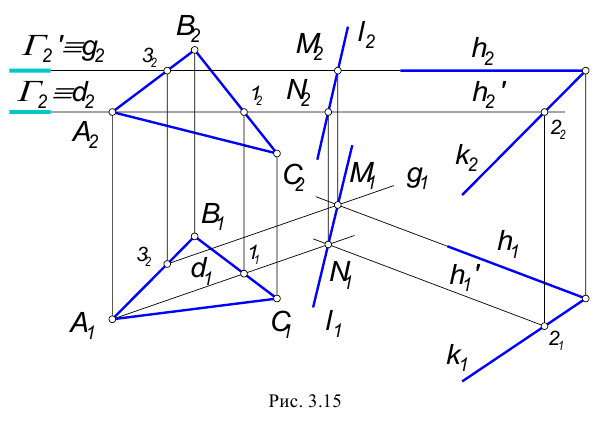
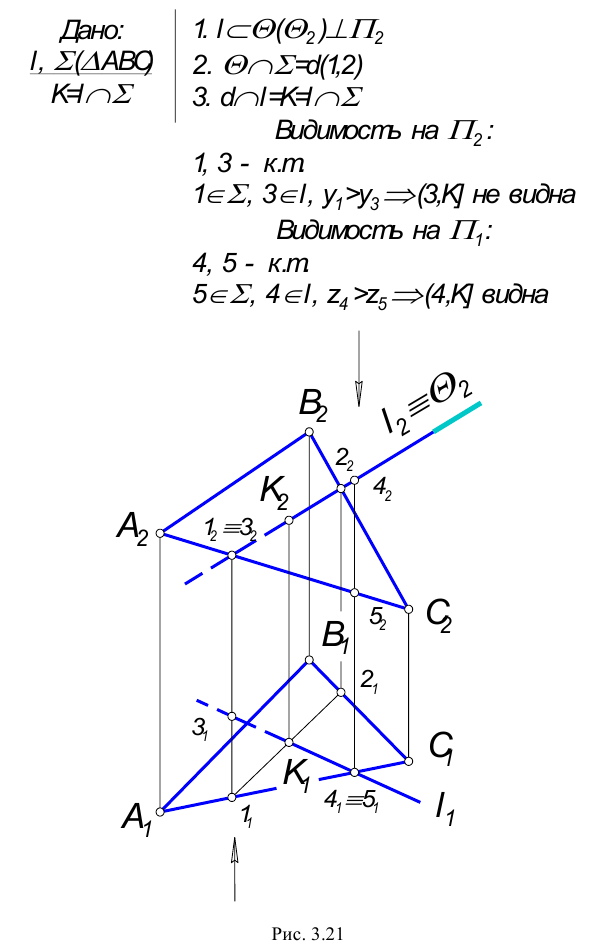
3. Пересекаются плоскости общего положения.
Определение видимости на КЧ
Для улучшения наглядности изображений, заданных на КЧ, принято видимые для наблюдателя линии показывать сплошными, а невидимые штриховыми линиями. При этом предполагается, что:
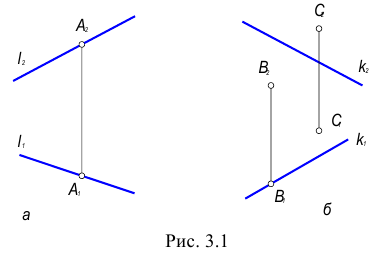
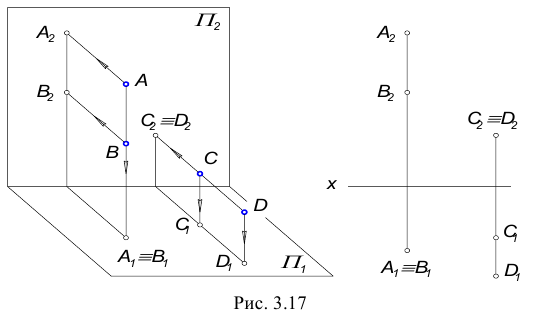
Даны две пары точек:
Необходимо определить видимость точек относительно горизонтальной и фронтальной плоскостей проекций.
Если на КЧ какие-либо две проекции точек совпадают, то для наблюдателя будет видима та точка, проекция которой на КЧ находится дальше от оси проекций.
Точки А и В, С и D называются точками, конкурирующими в видимости, а сам метод определения видимости – метод конкурирующих точек.
Конкурирующими в видимости точками называются точки, лежащие на одном проецирующем луче, но принадлежащие разным геометрическим объектам.
Пересечение прямой с плоскостью
Прямая называется пересекающей плоскость, если она имеет с ней только одну общую точку. Рассмотрим различные случаи пересечения прямой и плоскости,
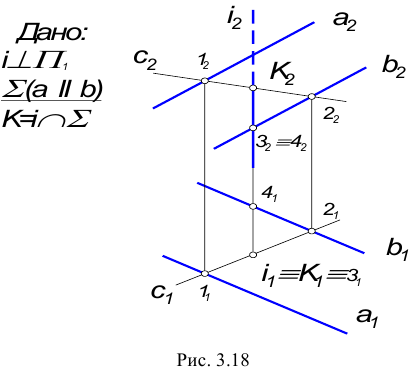
1. Прямая – проецирующая, плоскость – частного положения.
На КЧ необходимо построить проекции точки пересечения прямой с плоскостью и определить видимость этой прямой относительно горизонтальной и фронтальной плоскостей проекций. Точка К должна одновременно принадлежать и прямой, и плоскости.
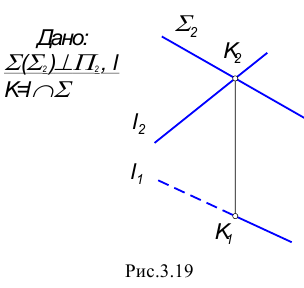
В данном случае фронтальная проекция точки пересечения лежит на следе плоскости
Построение недостающей горизонтальной проекции точки пересечения сводится к задаче на принадлежность точки прямой:
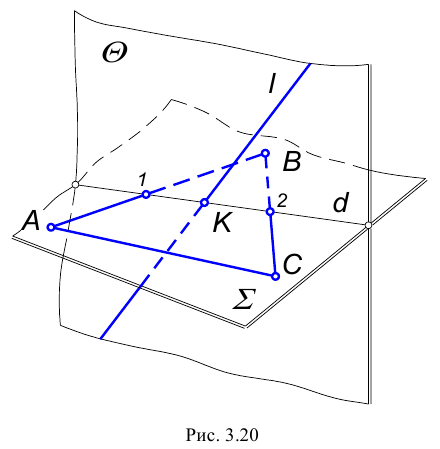
Пересечение прямой общего положения с плоскостью общего положения (первая основная позиционная задача).
В общем случае задача на пересечение прямой с плоскостью решается с помощью вспомогательной секущей плоскости, на которую накладывается ряд условий:
Порядок нахождения точки пересечения прямой с плоскостью:
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Аксиомы стереометрии. Взаимное расположение двух прямых, прямой и плоскости, двух плоскостей в пространстве
Стереометрия – это раздел геометрии, в котором изучаются свойства фигур в пространстве. Слово «стереометрия» происходит от греческих слов «στερεοσ» – объемный, пространственный и «μετρεο» – измерять.
Плоскость
Представление о плоскости дает поверхность стола или стены, любая гладкая поверхность. Плоскость как геометрическую фигуру надо представлять себе как бесконечно неограниченную во все стороны поверхность.
Аксиомы стереометрии и их следствия
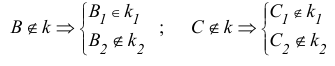

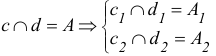
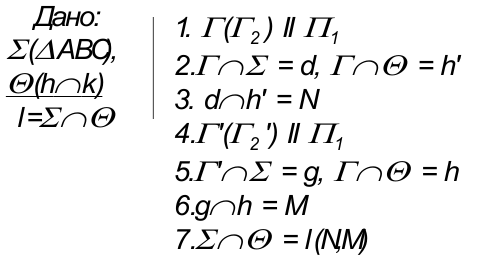
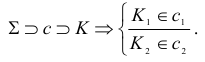
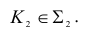
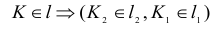

 Вам будет интересно: Пополняем словарный запас: неказистый — это.
Вам будет интересно: Пополняем словарный запас: неказистый — это. Вам будет интересно: «Соразмерно» — это и «в рамках», и «гармонично»
Вам будет интересно: «Соразмерно» — это и «в рамках», и «гармонично» Вам будет интересно: Обзор основных вузов Сургута
Вам будет интересно: Обзор основных вузов Сургута