Гистограмма что это такое в статистике
Конспект курса «Основы статистики»
1. Введение
Способы формирования репрезентативной выборки:
Простая случайная выборка (simple random sample)
Стратифицированная выборка (stratified sample)
Групповая выборка (cluster sample)
Типы переменных:
непрерывные (рост в мм)
дискретные (количество публикаций у учёного)
Ранговые (успеваемость студентов)
Гистограмма частот:
Позволяет сделать первое впечатление о форме распределения некоторого количественного признака.
Описательные статистики:
Меры центральной тенденции (узкий диапазон, высокие значения признака):
( используется для среднего значения из выборки, а для генеральной совокупности латинская буква
)
Свойства среднего:
Если к каждому значению выборки прибавить определённое число, то и среднее значение увеличится на это число.
Если к каждому значению выборки прибавить определённое число, то и среднее значение увеличится на это число.
Если для каждого значения выборки, рассчитать такой показатель как его отклонение от среднего арифметического, то сумма этих отклонений будет равняться нулю.
Меры изменчивости (широкий диапазон, вариативность признака):
При добавлении сильно отличающегося значения данные меняются сильно и могут быть некорректные.
Дисперсия генеральной совокупности:
(среднеквадратическое отклонение генеральной совокупности)
(среднеквадратическое отклонение выборки)
Свойства дисперсии:
Квартили распределения и график box-plot

Нормальное распределение
Отклонения наблюдений от среднего подчиняются определённому вероятностному закону.
Стандартизация
Правило «двух» и «трёх» сигм
Центральная предельная теорема
Есть признак, распределенный КАК УГОДНО* с некоторым средним и некоторым стандартным отклонением. Тогда, если выбирать из этой совокупности выборки объема n, то их средние тоже будут распределены нормально со средним равным среднему признака в ГС и стандартным отклонением .
30″ alt=»SE = \frac
Доверительные интервалы для среднего
Доверительный интервал является показателем точности измерений. Это также показатель того, насколько стабильна полученная величина, то есть насколько близкую величину (к первоначальной величине) вы получите при повторении измерений (эксперимента).
Идея статистического вывода
2. Сравнение средних
T-распределение
Если число наблюдений невелико и \sigma неизвестно (почти всегда), используется распределение Стьюдента (t-distribution).
Унимодально и симметрично, но: наблюдения с большей вероятностью попадают за пределы от
«Форма» распределения определяется числом степеней свободы ().
С увеличением числа распределение стремится к нормальному.
t-распределение используется не потому что у нас маленькие выборки, а потому что мы не знаем стандартное отклонение в генеральной совокупности.
Сравнение двух средних; t-критерий Стьюдента
Критерий, который позволяет сравнивать средние значения двух выборок между собой, называется t-критерий Стьюдента.
Условия для корректности использования t-критерия Стьюдента:
Две независимые группы
Формула стандартной ошибки среднего:
Формула числа степеней свободы:
Формула t-критерия Стьюдента:
Переход к p-критерию:
Проверка распределения на нормальность, QQ-Plot
Однофакторный дисперсионный анализ
Часто в исследованиях необходимо сравнить несколько групп между собой. В таком случае применятся однофакторный дисперсионный анализ.
Группы:
Нулевая гипотеза:
Альтернативная гипотеза:
Среднее значение всех наблюдений:
Общая сумма квадратов (Total sum of sqares):
Показатель, который характеризует насколько высока изменчивость данных, без учёта разделения их на группы.
Число степеней свободы:
— Межгрупповая сумма квадратов (Sum of sqares between groups)
— Внутригрупповая сумма квадратов (Sum of sqares within groups)
F-значение (основной статистический показатель дисперсионного анализа):
При делении значения межгрупповой суммы квадратов на число степеней свободы, полученный показатель усредняется.
Поэтому формула F-значения часто записывается:
Множественные сравнения в ANOVA
Проблема множественных сравнений:
Поправка Бонферрони
Самый простой (и консервативный) метод: P-значения умножаются на число выполненных сравнений.
Критерий Тьюки
Критерий Тьюки используется для проверки нулевой гипотезы против альтернативной гипотезы
, где индексы
и
обозначают любые две сравниваемые группы.
Указанные сравнения выполняются при помощи критерия Тьюки, который представляет собой модифицированный критерий Стьюдента:
где — рассчитываемая в ходе дисперсионного анализа внутригрупповая дисперсия.
Многофакторный ANOVA
При применении двухфакторного дисперсионного анализа исследователь проверяет влияние двух независимых переменных (факторов) на зависимую переменную. Может быть изучен также эффект взаимодействия двух переменных.
Исследуемые группы называют эффектами обработки. Схема двухфакторного дисперсионного анализа имеет несколько нулевых гипотез: одна для каждой независимой переменной и одна для взаимодействия.
Условия применения двухмерного дисперсионного анализа:
Генеральные совокупности, из которых извлечены выборки, должны быть нормально распределены.
Выборки должны быть независимыми.
Дисперсии генеральных совокупностей, из которых извлекались выборки, должны быть равными.
Группы должны иметь одинаковый объем выборки.
АБ тесты и статистика
3. Корреляция и регрессия
Понятие корреляции
Коэффициент корреляции – это статистическая мера, которая вычисляет силу связи между относительными движениями двух переменных.
Принимает значения [-1, 1]
— показатель силы и направления взаимосвязи двух количественных переменных.
Знак коэффициента корреляции показывает направление взаимосвязи.
Коэффициент детерминации
— показывает, в какой степени дисперсия одной переменной обусловлена влиянием другой переменной.
Равен квадрату коэффициента корреляции.
Принимает значения [0, 1]
Условия применения коэффициента корреляции
Для применения коэффициента корреляции Пирсона, необходимо соблюдать следующие условия:
Сравниваемые переменные должны быть получены в интервальной шкале или шкале отношений.
Распределения переменных и
должны быть близки к нормальному.
Число варьирующих признаков в сравниваемых переменных и
должно быть одинаковым.
Коэффициент корреляции Спирмена
Регрессия с одной независимой переменной
Уравнение прямой:
— (intersept) отвечает за то, где прямая пересекает ось y.
— (slope) отвечает за направление и угол наклона, образованный с осью x.
Метод наименьших квадратов
Формула нахождения остатка:
— остаток
— реальное значение
— значение, которое предсказывает регрессионная прямая
Сумма квадратов всех остатков:
Параметры линейной регрессии:
Гипотеза о значимости взаимосвязи и коэффициент детерминации
Коэффициенты линейной регрессии
Коэффициенты регрессии (β) — это коэффициенты, которые рассчитываются в результате выполнения регрессионного анализа. Вычисляются величины для каждой независимой переменной, которые представляют силу и тип взаимосвязи независимой переменной по отношению к зависимой.
Коэффициент детерминации
— доля дисперсии зависимой переменной (Y), объясняем регрессионной моделью.
— сумма квадратов остатков
— сумма квадратов общая
Условия применения линейной регрессии с одним предиктором
Линейная взаимосвязь и
Нормальное распределение остатков
Регрессионный анализ с несколькими независимыми переменными
Множественная регрессия (Multiple Regression)
Множественная регрессия позволяет исследовать влияние сразу нескольких независимых переменных на одну зависимую.
Требования к данным
линейная зависимость переменных
нормальное распределение остатков
проверка на мультиколлинеарность
нормальное распределение переменных (желательно)
Гистограмма
Гистограмма, это способ представления статистических данных в графическом виде – в виде столбчатой диаграммы. Она отображает распределение отдельных измерений параметров изделия или процесса. Иногда ее называют частотным распределением, так как гистограмма показывает частоту появления измеренных значений параметров объекта.
Высота каждого столбца указывает на частоту появления значений параметров в выбранном диапазоне, а количество столбцов – на число выбранных диапазонов.
Важное преимущество гистограммы заключается в том, что она позволяет наглядно представить тенденции изменения измеряемых параметров качества объекта и зрительно оценить закон их распределения. Кроме того, гистограмма дает возможность быстро определить центр, разброс и форму распределения случайной величины. Строится гистограмма, как правило, для интервального изменения значений измеряемого параметра.
Порядок построения гистограммы следующий:
1. Собираются статистические данные – результаты измерений параметра объекта. Для того, чтобы гистограмма позволяла оценить вид распределения случайной величины предпочтительно иметь не менее тридцати результатов измерений.
2. Выявляется наибольшее и наименьшее значение показателя среди полученных результатов измерений.
3. Определяется ширина диапазона значений показателя – из наибольшего значения показателя вычитается наименьшее значение.
4. Выбирается надлежащее число интервалов в пределах которых необходимо сгруппировать результаты измерений.
5. Устанавливаются границы интервалов. Границы интервалов необходимо установить так, чтобы значения данных не попадали ни на одну из границ интервала. Например, если были выбраны интервалы с границами от 0,5 до 5,5 от 5,5 до 10,5 и т.д. то значение данных 5,5 будет попадать как в первый, так и во второй интервал. Чтобы избежать этой проблемы можно изменить интервалы от 0,51 до 5,50 от 5,51 до 10,50 и так далее, таким образом ни одно значение данных не попадет на границу интервала.
6. Подсчитывается число попаданий значений результатов измерений в каждый из интервалов.
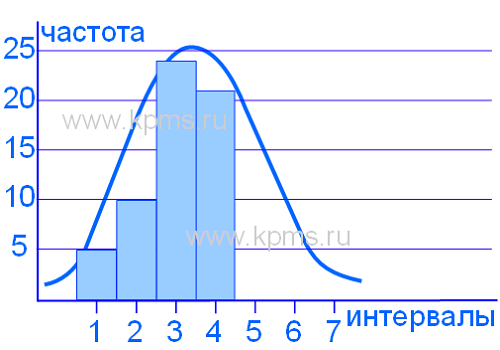
7. Строится гистограмма – на оси абсцисс (горизонтальной оси) отмечаются интервалы, а на оси ординат (вертикальной оси) отмечается частота попаданий результатов измерений в каждый интервал. Интервалы можно устанавливать в натуральных единицах (если позволяет масштаб), т.е. в тех единицах, в которых проводились измерения, либо каждому интервалу можно присвоить порядковый номер и отмечать на оси абсцисс номера интервалов. В результате получается столбчатая диаграмма, представленная на рисунке ниже.
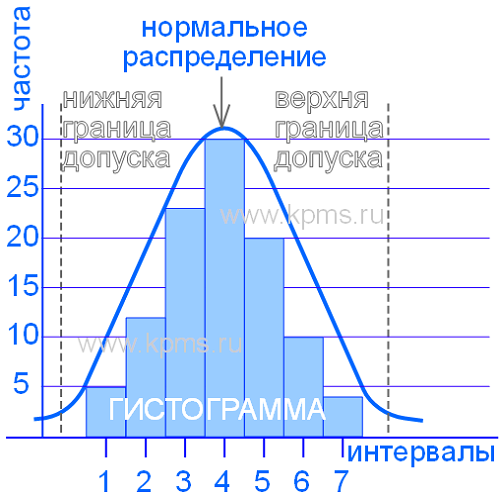
Если на контролируемый параметр существует поле допуска, то гистограмма может содержать верхнюю и нижнюю границы поля допуска. Это позволяет увидеть в какую сторону и как смещается значение контролируемого показателя относительно поля допуска. Границы наносятся по оси абсцисс.
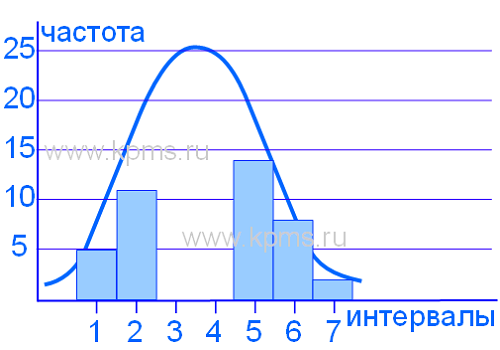
Гистограмма, представленная на рисунке выше имеет форму нормального распределения, что говорит о стабильности процесса, но часто бывает, что форма распределения отклоняется от нормального. Это свидетельствует о нарушениях в процессе и необходимости применения управляющих воздействий.
Некоторые, часто встречающие отклонения и их причины представлены ниже.
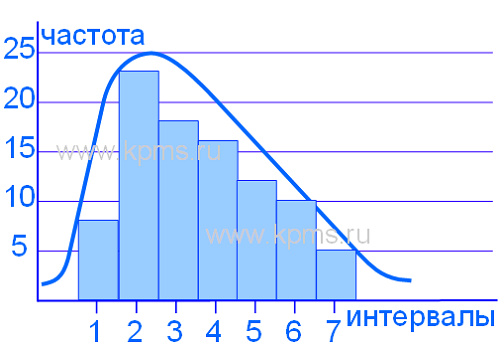
Гистограмма смещена влево (асимметрия влево):
Может вызываться смещением процесса к верхней границе допуска, либо из множества измерений отсортированы результаты, которые выпадают за пределы верхней границы допуска, либо природа процесса физически запрещает любые измерения больше чем максимальные значения допуска.
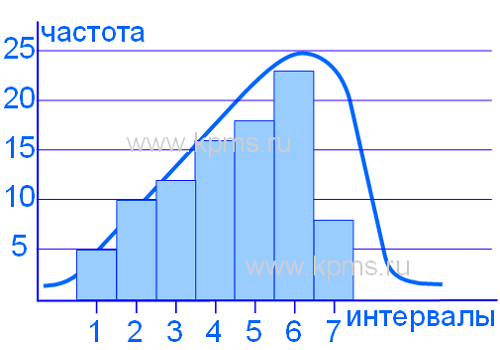
Гистограмма смещена вправо (асимметрия вправо):
Может вызываться смещением процесса к нижней границе допуска, либо из множества измерений отсортированы результаты, которые выпадают за пределы нижней границы допуска, либо природа процесса физически запрещает любые измерения меньше чем минимальные значения допуска.
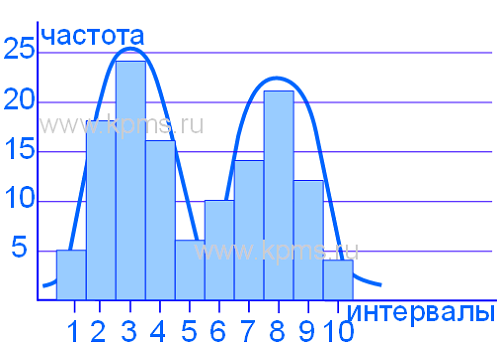
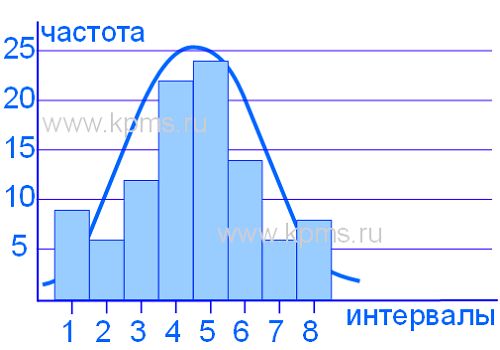
Гистограмма отображает два совмещенных процесса. Такая ситуация может произойти если результаты измерений получены от двух разных устройств, двух операторов, контролеров, разных измерительных инструментов, или с разных точек измерения.
Распределение не является нормальным т.к. нет постепенного снижения частоты результатов измерений от центра к границам допуска. Такой вид гистограммы возникает если процесс не способен удовлетворять спецификациям и часть измерений отсортирована с двух сторон при приближении к границам допуска, либо потеряны чересчур малые значения результатов измерений.
Гистограмма не имеет центра:
Центр распределения был отсортирован из набора данных результатов измерений. Такая ситуация может возникнуть из-за недостаточных требований в инженерной спецификации.
Гистограмма содержит выступы на границах:
Часть измерений на удаленных от центра сторонах распределения была изменена, чтобы привести характеристики процесса в соответствие с установленным полем допуска или измерения, выходящие за пределы поля допуска были записаны как входящие в поле допуска.
Сильные стороны гистограммы, как инструмента контроля качества, заключаются в ее наглядности, простоте, возможности быстро представить вид распределения большого числа данных. Также гистограмма показывает взаимосвязь изменения контролируемых параметров по отношению к инженерным спецификациям.
К недостаткам можно отнести – отсутствие возможности количественно оценить стабильность процесса, отсутствие привязки ко времени, необходимость большого числа данных для точной оценки структуры распределения, возможность различного толкования результатов, некоторая субъективность в представлении формы распределения.
Инструмент «гистограмма» входит в состав сборника «Семь инструментов качества». Сборник можно приобрести в интернет-магазине «Менеджмент качества».
Семь инструментов качества
Семь инструментов качества
Брошюра «Семь инструментов качества» содержит справочную информацию об основных инструментах менеджмента качества. В брошюре представлено описание и даны примеры применения следующих инструментов менеджмента качества: