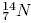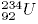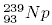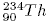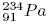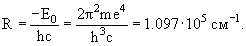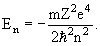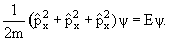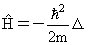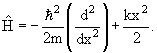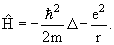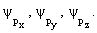чем больше номер стационарной боровской орбиты в атоме тем
Постулаты Бора.
Основой квантовой теории атома Бора являются 2 постулата.
Первый постулат Бора: атомная система может находиться только в особых стационарных, либо квантовых, состояниях, каждому из которых соответствует некоторая энергия En; в стационарном состоянии атом не излучает энергию.
Этот постулат является противоречием классической механике, согласно которой энергия движущихся электронов может быть любой. Также он является противоречием и электродинамике Максвелла, т.к. предполагает возможность ускоренного движения электронов не излучая электромагнитных волн.
Второй постулат Бора: излучение света случается в процессе перехода атома из стационарного состояния с большей энергией Ek в стационарное состояние с меньшей энергией En. Энергия излученного фотона равняется разности энергий стационарных состояний:

Таким образом можно вычислить частоту излучения:

Поглощая свет атом переходит из стационарного состояния с меньшим количеством энергии в стационарное состояние с большим количеством энергии.
Модель атома водорода Бора.
Чтоб построить модель самой простой системы — атома водорода — Бор также постулировал правило определения стационарных значений энергии атома (уровней энергии) — правило квантования.
Стационарным состояниям атома идентичны разрешенные дискретные значения энергии электрона, такие, что при движении по стационарным круговым орбитам электрон может иметь дискретные значения момента количества движения:
r — является радиусом орбиты,
n является главным квантовым числом (номер орбиты в спектре атома водорода).
Правило квантования орбит и постулаты Бора дали ему и последующим ученым объяснить замеченные закономерности в оптическом спектре излучения атома водорода и в рентгеновских спектрах, и дать физическое толкование Периодического закона элементов Менделеева.
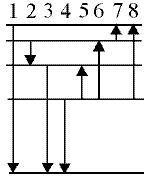
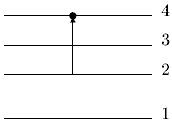
Поглощение света — является процессом, который обратен излучению, при котором атом с нижних энергетических уровней переходит на верхние уровни. В процессе чего он поглощает излучение таких же частот, которые излучает при переходе с верхних энергетических уровней на нижние. На рисунке б стрелками изображены переходы атома из одних состояний в другие с поглощением света.
B) на 4-й наименьшую, на 1-й наибольшую



Тест
Ядерная физика
A) 0,97 с
2. Укажите все верные утверждения. Чем больше номер стационарной боровской орбиты в атоме, тем…
1) больше кинетическая энергия электрона;
2) больше потенциальная энергия электрона;
3) больше заряд электрона;
4) больше полная энергия электрона;
5) больше скорость электрона.
D) 2 и 4
3. Сколько электронов содержится в электронной оболочке двухзарядного положительного иона гелия 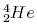
5. Каково соотношение между центростремительными ускорениями электрона a1, a2, a3 на трех стационарных боровских орбитах атома водорода a1 радиусы которых r123?
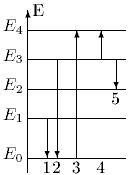
7. На рисунке представлена диаграмма энергетических уровней некоторого атома и несколько переходов между ними. Какой стрелкой указан переход с испусканием фотона наибольшей частоты?
8. Сколько электронов находится в электронной оболочке однозарядного положительного иона изотопа углерода 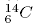
9. Чему равно число электронов в электронной оболочке атома изотопа кислорода 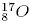
10. На рисунке представлена диаграмма энергетических уровней атома. Какой стрелкой обозначен переход с излучением фотона наибольшей частоты?
11. Из приведенных ниже утверждений укажите постулаты теории Бора.
1) в атомах есть избранные стационарные орбиты, двигаясь по которым электроны не излучают свет;
2) в атомах есть избранные стационарные орбиты, двигаясь по которым электроны излучают свет;
3) атомы излучают свет квантами при переходе с одной стационарной орбиты на другую;
4) при излучении света электроны движутся по спирали, постепенно теряя энергию и приближаясь к ядру.
B) 1 и 3
12. Какие утверждения относительно электрических свойств атома верны?
1) ядро атома заряжено положительно;
2) ядро атома заряжено отрицательно;
3) заряд электронной оболочки положителен;
4) заряд электронной оболочки отрицателен;
5) в ядре сосредоточен почти весь заряд атома;
6) в электронной оболочке сосредоточен почти весь заряд атома;
7) заряды ядра и электронной оболочки равны по величине и противоположны по знаку.
C) 1, 4 и 7
13. Какие из следующих утверждений не соответствуют модели атома Томпсона?
1) атом – положительно заряженный шар с равномерным распределением заряда по объему;
2) электроны распределены по поверхности положительно заряженного шара;
3) суммарный заряд электронов равен заряду шара;
4) атом – положительно заряженный шар, причем весь его положительный заряд распределен по поверхности шара;
5) электроны распределены по объему положительно заряженного шара.
A) 4 и 2
14. Какая часть атома вносит основной вклад в рассеяние альфа-частиц в опытах Резерфорда?
A) атомное ядро
B) отдельные протоны
C) отдельные электроны
D) электронная оболочка в целом
15. Сравните число электронов (n1 и n2) в электронных оболочках изотопов азота 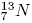
16. На рисунке представлена диаграмма энергетических уровней некоторого атома. Какой стрелкой обозначен переход с излучением фотона наибольшей частоты?
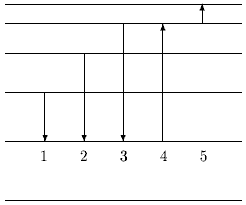
17.Атом возбуждается со второго на 4-й энергетический уровень, как это показано на рисунке. Сколько всего линий можно наблюдать в спектре излучения этого атома?
18. На какую стационарную орбиту переходят электроны в атоме водорода при испускании видимого света?
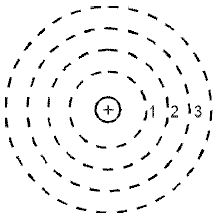
19. На рисунке изображены условные электронные орбиты атома. На каких орбитах электроны имеют наибольшую и наименьшую скорость?
A) на 4-й наибольшую, на 1-й наименьшую
B) на 4-й наименьшую, на 1-й наибольшую
C) на 3-й наибольшую, на 2-й наименьшую
D) на всех орбитах имеют одинаковую скорость
B) 75
C) 13,9
22. Энергия фотона, испускаемого атомом при переходе атома из состояния с энергией Е1 в состояние с энергией Е2 определяется выражением,…
23. Излучение лазера: 1) когерентно; 2) не когерентно; 3) монохроматично; 4) не монохроматично; 5) направленно; 6) изотропно.
C) 1, 3 и 5
24. Сколько всего нуклонов содержится в ядре атомов изотопа урана 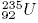
B) 235
25. Ядро урана 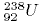
A)
B)
C)
D)
26. Сколько нейтронов содержится в ядре атома изотопа лития 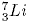
27. Сопоставьте величину ядерных сил, действующих внутри ядра между двумя протонами (Fpp), двумя нейтронами (Fnn), и между протоном и нейтроном (Fpn)
C) (Fpp) = (Fnn) = (Fpn)
28. Какой частицей бомбардирован дейтерий в ядерной реакции
B) гамма – квантом
29. Сколько энергии (Дж) выделят при аннигиляции 1 кг вещества и 1 кг антивещества. Скорость света с = 3•10 8 м/с.
A) 1,8•10 17
30. В начале наблюдения было 8 млн. радиоактивных ядер. Через 30 суток остался 1 млн. Чему равен период полураспада (сут) данного радиоактивного изотопа?
A) 10
31. Какое количество энергии (Дж) выделится при аннигиляции 2 г антивещества с 2 г вещества? Скорость света с = 3•10 8 м/с
A) 18•10 13
C) 21•10 25
C) 4•10 17
34. Что происходит с ядром в процессе альфа-распада?
Чем больше номер стационарной боровской орбиты в атоме тем
Исходя из представлений классической физики и дополнив ее квантовыми постулатами, Н. Бор создал модель атома, в которой электроны находились в определенных стационарных состояниях, что позволило объяснить устойчивость системы и дискретный характер атомных спектров. Опыты Франка-Герца подтвердили правильность модели Бора.
Однако непоследовательность теории, в которую квантованность состояний была введена искусственно, привела к необходимости разработки более рационального подхода к описанию квантовых явлений. Гипотеза де Бройля позволила создать аппарат волновой механики, в котором вероятностный характер квантовых явлений описывается с помощью волновых функций. Квадрат волновой функции определяет вероятность обнаружения частицы в элементе объема пространства dV. Волновая функция и квантовые операторы – аналоги физических величин в классической физике, описывают состояния частиц квантового мира.
Поведение системы квантовых частиц существенно отличается от классических закономерностей. Статистики Ферми-Дирака и Бозе-Эйнштейна позволяет объяснить структуру атомов и атомных ядер, парные корреляции в атомной и ядерной среде.
3.1. Модель Бора атома водорода
Основные постулаты теории Бора:
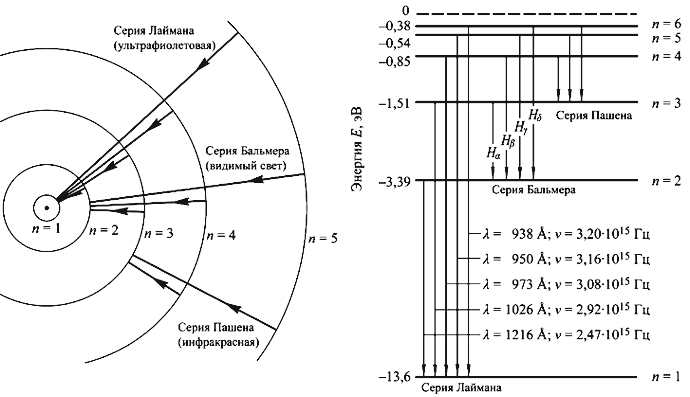
Рис. 3.1. Орбиты модели атома Бора. Схема уровней атома водорода.
Движение по круговой орбите. Частота обращения ν:
Условие стационарной орбиты. Квантование углового момента:
Боровский радиус атома водорода (n = 1, Z = 1) r0 = ћ 2 /me 2 = 0.529 Å
Полная энергия электрона E квантуется:
Если электрон находится на 1-ой боровской орбите, то атом водорода находится в основном состоянии E0 = −me 4 /2ћ 2 = −13.6 эВ.
Постоянная Ридберга
3.2. Рентгеновские спектры. Закон Мозли
В химических элементах электроны распределяются по электронным орбитам в соответствии с принципом Паули. Если из атома с орбиты n = 1 выбивается электрон, то вакансия заполняется электронами с более высоких орбит с n = 2, 3 и т. д. Разность энергий этих орбит излучается в виде фотонов, длина волны которых при больших Z будет находиться в рентгеновском диапазоне.
Закон Мозли. Согласно теории Н. Бора, энергия электрона на боровской орбите пропорциональна квадрату заряда ядра
Г. Мозли предположил, что энергия и, следовательно, частота характеристического излучения должны зависеть от квадрата атомного номера Z химического элемента.
Мозли измерил характеристическое рентгеновское излучение для нескольких десятков химических элементов и показал, что их можно аппроксимировать формулой ν 1/2 = A(Z – b), где ν – частота излучения, а A и b – константы, либо слабо изменяющиеся величины. Для линии Kα эта зависимость имеет вид:
где R – постоянная Ридберга, σ – постоянная экранирования, для легких элементов σ ≈ 1.
Исследования Мозли впервые экспериментально показали, что основной величиной, определяющей положение элемента в периодической таблице, является не атомная масса, а атомный номер химического элемента.
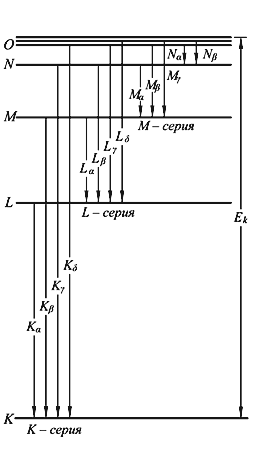 Рис. 3.2 Схема возникновения характеристических рентгеновских спектров. | 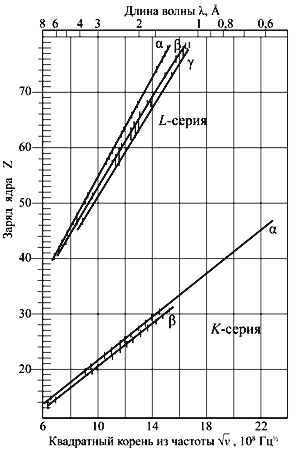 Рис. 3.3 График Мозли. Зависимость частоты рентгеновского излучения Kи L-серий от атомного номера химического элемента. |
3.3. Эксперименты Франка-Герца
Эксперименты Франка-Герца подтвердили предположение Бора о том, что спектры атомов объясняются наличием дискретных энергетических уровней, которые могут возбуждаться в результате рассеяния электронов на атоме.
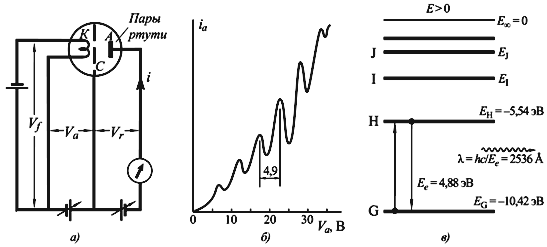
Энергии связи внешних электронов в тяжелых атомах составляют несколько эВ. На рис. 3.4 в показаны уровни энергии валентных электронов атома ртути. Энергия электронов основного состояния E0 = −10.42эВ. Энергия первого возбужденного состояния Eh = −5.54 эВ. Энергия перехода между этими состояниями
Если энергия пучка медленных электронов, проходящего через пары ртути, меньше 4.88 эВ, то столкновения электронов пучка с атомами ртути будут упругими, т.е. без передачи энергии. Если энергия пучка электронов превышает 4.88 эВ, то происходят неупругие столкновения с передачей части энергии электрону атома ртути, сопровождающиеся переходами электронов атома ртути в первое возбужденное состояние. Поэтому в зависимости анодного тока от ускоряющего потенциала будут наблюдаться характерные максимумы и минимумы, соответствующие дискретным уровням энергии, на которых находятся внешние электроны атома ртути.
Рис. 3.4 Опыт Франка-Герца. а) Схема экспериментальной установки. В баллоне с парами ртути имелись три электрода: К – катод, А – анод и С – сетка. Ускоряющая разность потенциалов Vaприкладывалась между катодом и сеткой, между сеткой и анодом создавалось тормозящее поле с
Vr = 0.5 В. б) Полученная зависимость анодного тока от Va. Интервал между максимумами составляет 4.9 В. в) Схема энергетических уровней ртути.
3.4. Состояния в классической и квантовой физике
Теория атома Н. Бора правильно описала переходы в атоме водорода. Значение радиуса первой боровской орбиты хорошо согласовывалось экспериментальными оценками размера атома водорода. Однако она не могла объяснить относительную интенсивность спектральных линий, а также структуру оптических спектров более сложных атомов. В своей теории Бор правильно предугадал основные особенности квантового строения атомов. Дальнейшее развитие квантовой физики показало, что описание состояний системы в классической и квантовой физике различны. Квантовые понятия отражают фактическую смену представлений о структуре материи, о свойствах ее фундаментальных составляющих. Поиски ответов на эти проблемы привели к новому пониманию природы материи и становлению квантовой физики.
Сопоставление способов описания частицы в классической и квантовой физике приведено в таблице.
Классическая физика






(не статистическое) описание
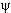 (x,y,z)| 2
(x,y,z)| 2 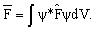
 =
= 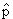 2 /2m + U(r)
2 /2m + U(r)3.5. Волновая функция
Состояние частицы в классической физике в любой момент времени описывается заданием ее координат и импульсов (x, y, z, px,py,pz). Зная эти величины в момент времени t, можно описать эволюцию системы под действием известных сил во все последующие и предыдущие моменты времени. Координаты и импульсы частиц в классической физике являются непосредственно измеряемыми величинам или наблюдаемыми.
В квантовой физике изменяется понятие состояния. Наличие у квантовой частицы волновых свойств показывает, что ей следует сопоставить некоторое волновое поле. Амплитуду этого волнового поля, зависящую от координат и времени, называют волновой функцией ψ(x,y,z,t). Волновая функция не является непосредственно наблюдаемой величиной. Наблюдаемой величиной является квадрат модуля волновой функции. В заданном состоянии с волновой функцией ψ(x,y,z,t) можно говорить только о вероятностном распределении значений наблюдаемых. Например, вероятность wнахождения частицы в данной точке x, y, z в момент времени tопределяется квадратом модуля волновой функции
В силу теории сложения вероятностей определение волновой функции необходимо дополнить условием нормировки
где интеграл, взятый по всему бесконечному пространству, − вероятность достоверно обнаружить частицу в момент времени t во всем пространстве. Возникает своеобразное двухступенчатое описание физических объектов: сначала нужно найти волновую функцию, а затем, уже по ней, определить значения наблюдаемых. В квантовой теории не все наблюдаемые одновременно могут иметь точно определенные значения. Например, квантовая частица не может иметь одновременно определенные значения импульса и координаты.
3.6. Уравнение движения свободной частицы
Волновая функция свободно движущейся частицы с энергией E и импульсом p имеет вид
Константа A определяется из условия нормировки волновой функции
В тех случаях, когда частица находится в области пространства, где действующие на нее силы равны нулю (свободное движение), энергия частицы может принимать любые значения. Энергетический спектр свободно движущейся частицы непрерывный.
Дифференциальное уравнение, которому удовлетворяет волновая функция свободно движущейся частицы, можно установить, дифференцируя волновую функцию ψ(r,t) по tи по переменным x, y, z:
Для свободной частицы
Из соотношений (3.8) и (3.9) с учетом (3.10) следует дифференциальное уравнение для волновой функции свободно движущейся частицы
Обычно (3.11) записывается в виде
где Δ − оператор Лапласа. Уравнение (3.12) в частных производных называется уравнением движения для свободной частицы. В уравнение движения (3.12) входит только такая характеристика как масса частицы и постоянная Планка ћ. Уравнение (3.12) является дифференциальным уравнением первого порядка по времени. Поэтому для определения волновой функции в произвольный момент времени t достаточно знать значение волновую функцию в начальный момент времени.
3.7. Физические величины и операторы
В квантовой механике постулируется, что каждой физической величине, описываемой в классической механике в виде функции F(x,y,z,px,py,pz) координат и импульсов ставится в соответствие линейный оператор 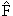






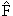
χ(x,y,z,t) = 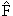
Например, оператор 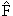
χ(x,y,z,t) = 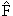
т. е. 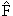
Оператор координаты 

Операторами проекций импульсов являются операторы
Для того, чтобы понять почему оператор импульса имеет вид (3.13), воспользуемся тем, что движение свободной частицы описывается уравнением
Оператор кинетической энергии 



поэтому операторы 


Остальные операторы могут быть построены с использованием операторов координаты и импульса согласно простому правилу: в квантовой механике операторы физических величин выражаются друг через друга так же, как сами физические величины в классической физике.
Оператор кинетической энергии 
Оператор Гамильтона (гамильтониан) − оператор полной энергии 



Если частица движется в потенциальном поле U (x, y, z), то оператор Гамильтона 
Оператор момента количества движения 
Согласно классической механике момент импульса 


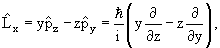 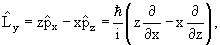 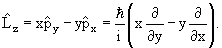 | (3.17) |
Оператор квадрата момента количества движения 
Гамильтониан



Частица в одномерной потенциальной яме U(x):
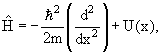
3.8. Собственные значения и собственные функции операторов
С каждым оператором 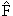
определяющее его собственные значения Fnи полную систему ортонормированных функций ψn, подчиняющихся определенным граничным условиям. Величины Fn определяют спектр возможных значений физической величины F. Функция ψn(x) характеризует состояние системы, в котором величина F имеет значение Fn. Одно из важнейших положений квантовой теории: в квантовых системах выполняется принцип суперпозиции. Если квантовая система может находиться в состояниях, описываемых функциями ψ1, ψ2, …, ψn, то линейная комбинация (суперпозиция) волновых функций ψ1, ψ2, …, ψn
также является волновой функцией, описывающей одно из возможных состояний системы, cn – произвольные постоянные.
Квантовая механика является принципиально статистической теорией. Её предсказания носят вероятностный характер. Можно с любой точностью предсказать вероятность найти электрон в произвольной части атома водорода, но нельзя предсказать, в какие моменты времени он попадает в эту часть атома.
Различие между классической статистической теорией и квантовой механикой состоит в следующем. В классической статистической теории предполагается, что в принципе можно проследить за судьбой, например, всех молекул газа и точно рассчитать их траектории. Но, так как молекул много, то для расчета макроскопических величин нам достаточно знать не все точные величины, описывающие каждую молекулу, а небольшое количество усредненных характеристик системы. Например, для описания газа, заключенного в сосуде, вводят такие усредненные характеристики как давление и температура. Для отдельной молекулы газа совершенно бессмысленно говорить о её температуре. В противоположность этому в квантовом мире статистические свойства не вторичны, а первичны. Статистический характер процессов в микромире проявляется в том, что результат измерений в микромире имеет статистическую природу.
Среднее значение физической величины А в состоянии ψ определяется из соотношения
где dV = dx dy dz. В частности, средние значения координаты 
Средние значения и
.
Уравнения для собственных функций и собственных значений операторов 


Решением уравнений будут волновые функции
где a(y,z), a(x,z), a(x,y) – произвольные функции соответствующих координат (y,z), (x,z), (x,y).
Оператор импульса имеет сплошной спектр собственных значений. Волновая функция
является собственной функцией операторов 



Постоянная A находится из условия нормировки волновой функции:
Волновая функция ψp с учетом нормировки имеет вид.
3.9. Коммутация операторов
Одним из важных вопросов в квантовой физике является вопрос о том, какие физические величины могут одновременно иметь определённые значения. Для того чтобы две величины F и R могли бы иметь определенные значения в некотором состоянии, описываемом волновой функцией ψn, эта волновая функция, очевидно, должна быть собственной функцией операторов 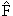
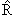
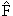
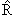
Это имеет место только в том случае, когда операторы 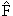
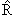
[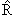 , ,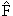 ] = ] = 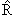 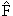 − − 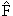 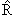 = 0. = 0. | (3.27) |
Таким образом, если квантовомеханические операторы, соответствующие двум квантовомеханическим величинам, коммутируют, то эти величины могут быть измерены одновременно. Если же операторы не коммутируют, то это величины одновременно не могут иметь определенных значений. Операторы координат и проекции импульса на различные оси коммутируют между собой. Например,



т. е. величины x и py одновременно измеримы.
В то же время операторы 
















т. е. квадрат полного момента количества движения и одна из его проекций на произвольную ось могут одновременно иметь определенные значения.
3.10. Статистики Ферми-Дирака и Бозе-Эйнштейна
Принцип тождественности частиц
Гамильтониан системы частиц инвариантен относительно перестановки всех координат двух любых частиц одного типа.
Поэтому должна быть квантовая характеристика (квантовое число) и сохраняющаяся физическая величина, отвечающая этому преобразованию.
Оператор перестановки (например, частиц 1 и 2 в системе А тождественных частиц) 
 12ψ(1,2. A) = ψ(2,1. A) = εψ(1,2. A), 12ψ(1,2. A) = ψ(2,1. A) = εψ(1,2. A), 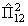 ψ(1,2. A) = ε 2 ψ(2,1. A) = ψ(1,2. A). ψ(1,2. A) = ε 2 ψ(2,1. A) = ψ(1,2. A). | (3.28) |
Поэтому ε 2 =1 и ε = ±1.
При e = +1 
волновая функция системы частиц симметрична:
ψ(2,1. A) = ψ(1,2. A).
При e = −1 
волновая функция системы частиц антисимметрична:
ψ(2,1. A) = −ψ(1,2. A).
В релятивистской квантовой теории поля доказывается, что статистика однозначно определяется спином частицы. Частицы с целым (в том числе с нулевым) спином называются бозонами и подчиняются статистике Бозе-Эйнштейна (γ‑кванты, π-мезоны, α-частицы и др.). Частицы с полуцелым спином называются фермионами и подчиняются статистике Ферми-Дирака (электроны, кварки, нейтрино, протоны, нейтроны, ядра с нечётным числом нуклонов и т.д.).
| Фермионы | Бозоны |
|---|---|
| электрон, мюон, нейтрино, протон, нейтрон и др. | фотон, π-мезоны, K-мезоны и др |
| Вероятность ƒ(E) обнаружить частицу в состоянии с энергией Eпри температуре среды T | |
| Распределение Больцмана | 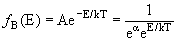 |
| Распределение Бозе-Эйнштейна | 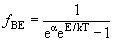 |
| Распределение Ферми-Дирака | 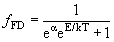 |
| Величина e α представляет собой постоянную нормировки, зависящую от плотности частиц | |
3.11. Принцип Паули для тождественных фермионов.
Для системы тождественных фермионов
Структура электронных оболочек в атоме и нуклонных оболочек в ядре объясняется на основе принципа Паули. В атоме два электрона не могут находиться в одинаковом состоянии. Точно так же и в ядре два одинаковых нуклона не могут находиться в одном и том же состоянии. Принципу Паули подчиняются только фермионы.
Задачи
3.1. Вычислите длину волны спектральной линии, которая соответствует переходу между состояниями ni = 4 и nf = 2 в атоме водорода.
3.2. У водородоподобного иона разница длин волн первых линий серий Лаймана и Бальмера составляет 16.58 нм. Какому атому это соответствует?
3.3. Минимальная длина волны излучения рентгеновской трубки на 50 кВ составляет 0.247 Å.
Определите значение постоянной Планка.
3.4. Вычислить разность энергий связи Kи L электронов в атоме алюминия 13 Al.
3.5. Вычислить коммутатор [





3.6. Какую максимальную энергию может иметь фотон, испущенный атомом водорода?
Ответ: Eγ = 13.6 В
3.7. Определить длину волны первых трех линий серий Бальмера, Лаймана, Пашена в атоме водорода.
3.8. Какому переходу соответствует длина волны линии Бальмера λ = 3791 Å в атоме водорода?
Ответ: Переход 10 → 2
3.9. Какие спектральные линии появятся при возбуждении атомарного водорода электронами в 12.5 В? Какие линии появятся при энергии электронов в 14 В?
3.10. Мюон образовал мезоатом водорода. Вычислите радиус первой боровской орбиты моюнного атома и сравните с результатом для атома водорода. Каковы длины волн первых трех линий серии Лаймана мезоатома?
Ответ: rμ = ћ 2 /me 2 = 255 Фм; E21 = 2.11 кэВ, E31 = 2.50 кэВ, E41 = 2.64 кэВ.
3.11. Позитроний представляет собой связанную систему электрона и позитрона, вращающихся вокруг центра масс этой системы. Определить боровский радиус и энергетический спектр позитрония. Каковы длины волн первых трех линий серии Лаймана позитрония?
3.12. Энергия связи электрона в атоме гелия He равна E0 = 24.6 эВ. Какая минимальная энергия необходима для последовательного удаления обоих электронов из этого атома?
3.13. Покажите, что скорость электрона v на n-Боровской орбите в атоме водорода равна v/c = α/n, где α – постоянная тонкой структуры.
3.14. Ток, возникающий при движении заряда q по круговой орбите с частотой f, равен i = qf. Магнитный момент μ петли с током равен μ = is, где s – площадь петли. Вычислите ток и магнитный момент, создаваемый электроном на первой боровской орбите.
3.15. Определить магнитный момент мюона, находящегося на первой боровской орбите в мюоном атоме, состоящем из протона и мюона. Сравнить с магнитным моментом электрона, находящимся в атоме водорода на первой боровской орбите.
3.16. Закон Мозли для характеристического рентгеновского излучения имеет следующую форму:
ν 1/2 = A(Z − b). Получите выражение и рассчитайте A для линий Kα.
Ответ: A = 4.9·10 7 с –1/2
3.17. Какова минимальная длина волны излучения, испускаемого рентгеновской трубкой при напряжении 30 кВ?
Ответ: λγ = 4.2·10 4 Фм
3.18. Определите порядковый номер Z легкого элемента, у которого длина волны Kα λ = 0.251 нм.
Ответ: Z = 23
3.20. Сколько химических элементов содержится в ряду между химическими элементами, у которых длины волн Kα линии равны 0.1787 нм и 0.1334 нм. Какие это химические элементы?
Ответ: от 27 Co до 30 Zn
3.21. Какие физические величины могут быть одновременно измерены в квантовой физике?
3.22. Вычислить коммутаторы: a) [














л) [



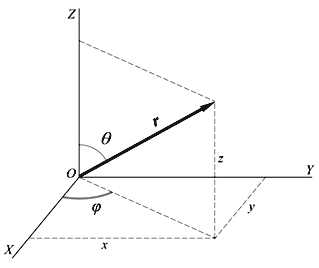 Рис. 3.5.Прямоугольная и сферическая системы координат |
3.23. При решении конкретных физических задач часто приходится иметь дело с полями с центральной симметрией. В таких случаях удобнее использовать сферическую систему координат. Переход от декартовых координат x, y, z к переменным r, θ, φ в операторах также происходит по обычным правилам замены переменных.
x = r sinθ cosφ, y = r sinθ sinφ, z = r cosφ.
Показать, что в сферической системе координат оператор момента количества движения имеет вид: