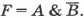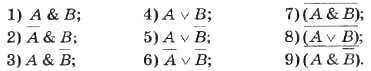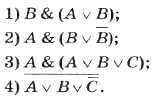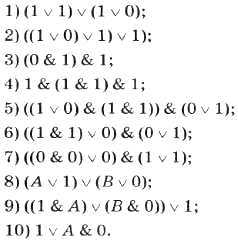Вот что отвечает лиз ане к уроку 26
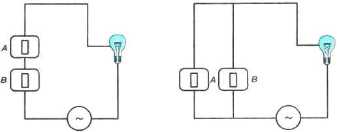
Вот что отвечает Лиз Ане?
Вот что отвечает Лиз Ане.
Как ты думаешь, какие вопросы Аня задает Лиз?
? They are white, grey and blak.
? Yes, she likes her kittens very mach.
Have you got a cat?
Has she got kittens?
How many kittens has she got?
What colour are they?
They are white, grey and black.
Does she like her kittens?
Yes, she likes her kittens very much.
Помогите, пожалуйста, составить вопросы на существующие ответы?
Помогите, пожалуйста, составить вопросы на существующие ответы.
(Диалог между девочками)
Pussy has got three kittens.
They are white, grey and black.
Yes, she likes her kittens very much.
Догадайся, какие вопросы мистер Гринвуд задал своим ученикам?
Догадайся, какие вопросы мистер Гринвуд задал своим ученикам?
Прочитай ответы запиши вопросы.
1) No, I dont like autumn.
We play tennis in summer.
I can ski and skate.
He has got a nice bike.
Did she win the tournament?
Did she win the tournament?
Yes, she is No, she does not Yes, she does No, she does not Yes, she did.
Напишите вопросы по ответам : 1?
Напишите вопросы по ответам : 1.
No, I don’t like autumn.
We play tennis in summer.
I can ski and skate.
He has got a nice bike.
Дайте краткий ответ?
Дайте краткий ответ.
1. Are they at home?
2. Is she at school?
4. Have they got a toy?
5. Has he got a sister?
Допишите вопросы и ответы.
Mary got five pens?
The kittens in the basket?
The kittens got a basket?
Помогите ответить на вопросы?
Помогите ответить на вопросы!
Has Tina got any English friends?
Догадайся, какие вопросы мистер Гринвуд задал своим ученикам?
Догадайся, какие вопросы мистер Гринвуд задал своим ученикам?
Прочитай ответы, запиши вопросы.
We play tennis in summer.
I can ski and skate.
He has got a nice bike.
Задай краткие вопросы кNo, they aren tYes, she isYes, he isNo, shi isn tYes, they are?
Задай краткие вопросы к
Дописать вопросы и ответыThey like chess?
Дописать вопросы и ответы
Помогите пожалуйста 12?
Помогите пожалуйста 12.
Допишите вопросы и ответы.
1) Alice cried that she was opening like a large telescope. 2) The Rabbit said that the Duchess would be so angry with him. 3) Alice asked the Rabbit if he could help her. 4) The poor child that he was too small and he couldn’t get to the key.
Я в италии. Я приехал с родителями на машине. Мы остановились в гостинице Хилтон. Наш отель рядом с супермаркетом напротив кинотеатра. Шас мы собираемся в кафе за ужином. Мне нравится итальянская еда особенно пицца.
Horoscope on April 2, 2017 Aries This day will require you seriously. All your rash decisions or impulsive actions can lead to unpredictable results. Life potential today you will be at a high level, however, due to conflicting trends luck at any m..
Where does they live? What does stories Sam like? Who likes adventure stories? Whom does they want to find? Who needs help.
Ona : Я никогда не встречал никого, кто любит каждую минуту снимать фильм так же сильно, как и вы. Вы не слишком подчеркиваете, у вас всегда хорошее настроение. И у вас мало ритуалов в течение дня, что вы делаете с большим стилем, как будто вы праз..
A, any, a. The, this, a. The.
1) Where is the shelf? 2) Have you gota shelf? 3) There is a shelf on the wall. 4) Is the shelf beautifull? 5) There are a lot of books onthe shelf.
Ответы по параграфу 1.4 Элементы алгебры логики
Задание 1. Ознакомьтесь с материалами презентации к параграфу, содержащейся в электронном приложении к учебнику. Дополняет ли презентация информацию, содержащуюся в тексте параграфа?
Задание 2. Объясните, почему следующие предложения не являются высказываниями.
Задание 3. Приведите по одному примеру истинных и ложных высказываний из биологии, географии, информатики, истории, математики, литературы.
• География:
1) Столица Италии – Париж. (ЛОЖЬ, т.к. это Рим, а Париж во Франции)
2) Выделяют 4 основные стороны света – север, юг, запад, восток.
• Информатика:
1) Инверсия – это логическое отрицание.
2) Конъюнкция – это логическое сложение. (ЛОЖЬ, т.к. это дизъюнкция является логическим сложением)
• История:
1) Промышленная революция (конец XVIII – первая половина XIX в.) началась в Англии в последней трети XVIII в.
2) Во времена аграрной революции в Англии в конце XVIII века землей владели фермеры, которые сдавали ее в аренду за определенную плату. (ЛОЖЬ, т.к. владели лендлорды, а фермеры были арендаторы)
• Математика:
1) У треугольника 5 сторон.
2) Квадрат гипотенузы равен сумме квадратов двух катетов.
• Литература:
1) Народные частушки – небольшие лирические песни, обычно имеющие форму четырехстрочного рифмованного куплета.
2) Первые упоминания о частушках относятся к 60-м годам XII века. (ЛОЖЬ, т.к это поздний жанр, появившийся только в XIX веке)
Задание 4. В следующих высказываниях выделите простые высказывания, обозначив каждое из них буквой; запишите с помощью букв и знаков логических операций каждое составное высказывание.
1) Число 376 чётное и трёхзначное.
А = Число 376 чётное
В = Число 376 трёхзначное
A & B
2) Зимой дети катаются на коньках или на лыжах.
A = Зимой дети катаются на коньках
B = Зимой дети катаются на лыжах
A | B
3) Новый год мы встретим на даче или на Красной площади.
A = Новый год мы встретим на даче.
B = Новый год мы встретим на Красной площади.
A | B
4) Неверно, что Солнце движется вокруг Земли.
A = Солнце движется вокруг Земли
¬A
5) Земля имеет форму шара, который из космоса кажется голубым.
A = Земля имеет форму шара, который из космоса кажется голубым.
B = Шар из космоса кажется голубым.
A & B
6) На уроке математики старшеклассники отвечали на вопросы учителя, а также писали самостоятельную работу.
A = На уроке математики старшеклассники отвечали на вопросы учителя
B = На уроке математики старшеклассники писали самостоятельную работу
A & B
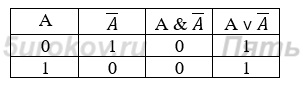
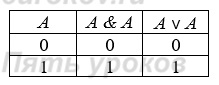
Задание 5. Постройте отрицания следующих высказываний.
Задание 6. Пусть А = «Ане нравятся уроки математики», а В = «Ане нравятся уроки химии». Выразите следующие формулы на обычном языке:
Задание 7. Некоторый сегмент сети Интернет состоит из 1000 сайтов. Поисковый сервер в автоматическом режиме составил таблицу ключевых слов для сайтов этого сегмента. Вот её фрагмент:
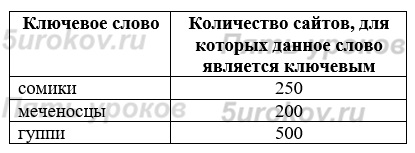
Дано дополнительно помимо таблицы:
сомики & гуппи – 0 сайтов;
сомики & меченосцы – 20 сайтов;
меченосцы & гуппи – 10 сайтов.
Нарисуем круги Эйлера:
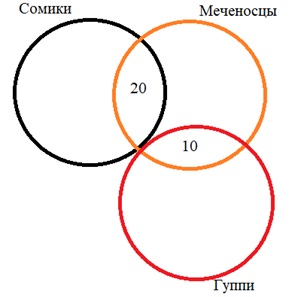
Чтобы найти количество сайтов, соответствующих этому запросу, к количеству элементов множества сомики (250) добавим количество элементов множества меченосцы без сомиков (200 – 20), а также гуппи без меченосцев (500 – 10).
Получаем: 250 + 180 + 490 = 920 сайтов
Ответ: 920 сайтов
2) Найти:
Для скольких сайтов рассматриваемого сегмента ложно высказывание «Сомики — ключевое слово сайта ИЛИ меченосцы — ключевое слово сайта ИЛИ гуппи — ключевое слово сайта»?
То есть это по сути всё, что не вошло в наш С | М | Г, то есть надо найти ¬(С | M | Г).
С | M | Г = 920
По условию задачи сегмент сети Интернет состоит из 1000 сайтов.
То есть, то, что не вошло в нашу область это 1000 – 920 = 80 сайтов.
Ответ: 80 сайтов
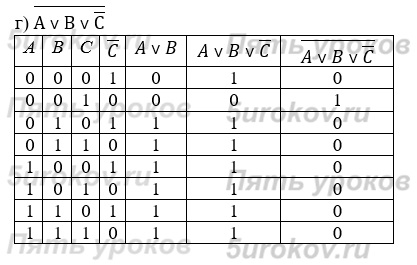
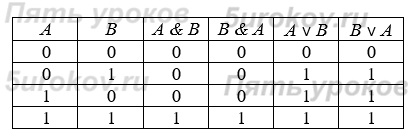
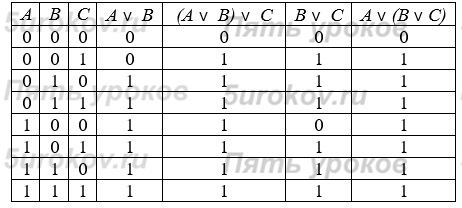
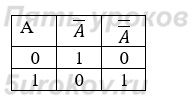
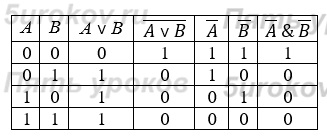
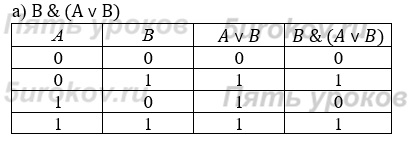
Задание 8. Постройте таблицы истинности для следующих логических выражений:
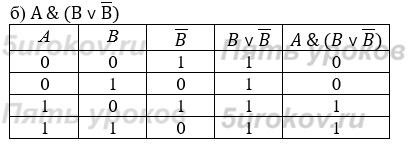
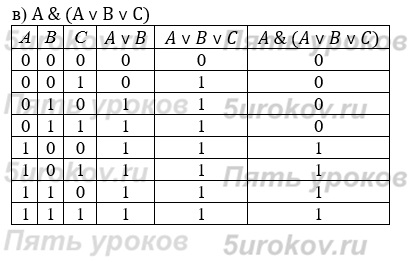
Задание 9. Проведите доказательство рассмотренных в параграфе логических законов с помощью таблиц истинности.
1) Переместительный (коммутативный) закон:
2) Сочетательный (ассоциативный закон):
для логического умножения:
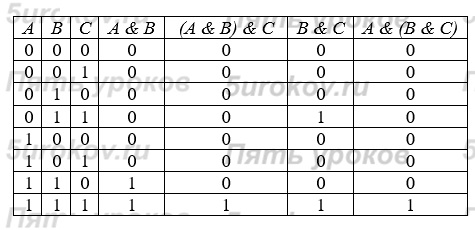
для логического сложения:
3) Распределительный (дистрибутивный) закон:
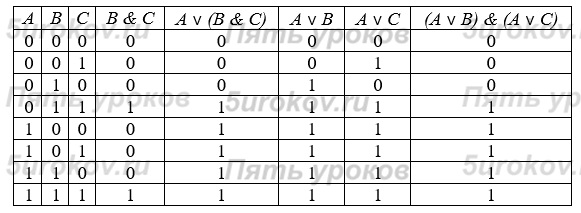
Совпадение значений в столбцах, соответствующих логическим выражениям в левой и правой частях равенства, доказывает справедливость распределительного закона для логического сложения.
4) Закон двойного отрицания:
5) Закон исключенного третьего:
6) Закон повторения:
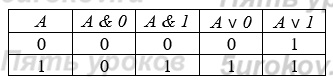
7) Закон операций с 0 и 1:
8) Законы общей инверсии:
а) для логического умножения:
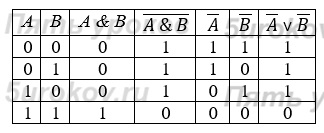
б) для логического сложения:
Задание 10. Даны три числа в десятичной системе счисления: A=23, B=19, C=26. Переведите A, B и C в двоичную систему счисления и выполните поразрядной логические операции (A ˅ B) & C. Ответ дайте в десятичной системе счисления.
Задание 11. Найдите значения выражений:
Задание 12. Найдите значение логического выражения для указанных значений числа Х:
а) 1; б) 2; в) 3; г) 4.
Задание 13. Пусть А = «Первая буква имени – гласная», В = «Четвертая буква имени согласная». Найдите значение логического выражения для следующих имён:
Задание 14. Разбирается дело Джона, Брауна и Смита. Известно, что один из них нашёл и утаил клад. На следствии каждый из подозреваемых сделал два заявления:
Смит: «Я не делал этого. Браун сделал это.»
Джон: «Браун не виновен. Смит сделал это.»
Браун: «Я не делал этого. Джон не делал этого.»
Суд установил, что один из них дважды солгал, другой дважды сказал правду, третий один раз солгал, один раз сказал правду. Кто из подозреваемых должен быть оправдан?
Задание 15. Алеша, Боря и Гриша нашли в земле старинный сосуд. Рассматривая удивительную находку, каждый высказал по два предположения. Где и в каком веке изготовлен сосуд?
Только в 1 прав, в другом не прав, следовательно, иcходя из 2 логических принципов составляем уравнение:
• 0 v 1 = 1
• 1 & 1=1
Усл. Обозначения:
Г – греческий, Ф – Финикийский, Цифра – век
(Г или 5)&(Ф или 3)&(неГ или 4)=1
Распределительный закон, раскрываем скобки:
(ГФ или Г3 или Ф5 или 53) & (неГ или 4)=1
ГФ и 53 обнуляем, т.к. это ложь (0), не может быть одновременно и то, и другое правдой. С тем, что осталось еще раз распределительный закон, раскрываем скобки:
(Г3 и неГ) или Г34 или (Ф5 и неГ) или Ф54 = 1
Г и неГ не может быть одновременно, обнуляем
Г34 обнуляем, Ф54 обнуляем.
Остается:
Ф5 и неГ = 1
Ответ: Финикийский сосуд, изготовлен в V веке.
Вот что отвечает лиз ане к уроку 26
Урок 11. Логические элементы. Решение логических задач.
Решение логических задач
Рассмотрим несколько способов решения логических задач.
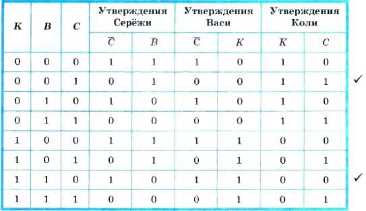
Задача 1. Коля, Вася и Серёжа гостили летом у бабушки. Однажды один из мальчиков нечаянно разбил любимую бабушкину вазу. На вопрос, кто разбил вазу, они дали такие ответы:
Серёжа: 1) Я не разбивал. 2) Вася не разбивал.
Вася: 3) Серёжа не разбивал. 4) Вазу разбил Коля.
Коля: 5) Я не разбивал. 6) Вазу разбил Серёжа.
Бабушка знала, что один из её внуков, назовём его правдивым, оба раза сказал правду; второй, назовём его шутником, оба раза сказал неправду; третий, назовём его хитрецом, один раз сказал правду, а другой раз — неправду. Назовите имена правдивого, шутника и хитреца. Кто из внуков разбил вазу?
1 С учётом того, что ваза разбита одним внуком, можно было составлять не всю таблицу, а только её фрагмент, содержащий следуюнще наборы входных переменных: 001, 010, 100.
Исходя из того, что знает о внуках бабушка, следует искать в таблице строки, содержащие в каком-либо порядке три комбинации значений: 00, 11, 01 (или 10). Таких строк в таблице оказалось две (они отмечены галочками). Согласно второй из них, вазу разбили Коля и Вася, что противоречит условию. Согласно первой из найденных строк, вазу разбил Серёжа, он же оказался хитрецом. Шутником оказался Вася. Имя правдивого внука — Коля.
Задача 2. В соревнованиях по гимнастике участвуют Алла, Валя, Сима и Даша. Болельщики высказали предположения о возможных победителях:
По окончании соревнований оказалось, что в каждом из предположений только одно из высказываний истинно, другое ложно. Какое место на соревнованиях заняла каждая из девушек, если все они оказались на разных местах?
Решение. Рассмотрим простые высказывания:
C1 = «Сима заняла первое место»;
В2 = «Валя заняла второе место»;
С2 = «Сима заняла второе место»;
Д3 = «Даша заняла третье место»;
А2 = «Алла заняла второе место»;
Д4 = «Даша заняла четвёртое место».
Так как в каждом из трёх предположений одно из высказываний истинно, а другое ложно, то можно заключить следующее:
Логическое произведение истинных высказываний будет истинным:
На основании распределительного закона преобразуем левую часть этого выражения:
Высказывание С1 • С2 означает, что Сима заняла и первое, и второе места. Согласно условию задачи, это высказывание ложно. Ложным является и высказывание В2• С2. Учитывая закон операций с константой 0, запишем:
Дальнейшее преобразование левой части этого равенства и исключение заведомо ложных высказываний дают:
Из последнего равенства следует, что С1 = 1, Д3 = 1, А2 = 1. Это означает, что Сима заняла первое место, Алла — второе, Даша — третье. Следовательно, Валя заняла четвёртое место.
Познакомиться с другими способами решения логических задач, а также принять участие в Интернет-олимпиадах и конкурсах по их решению вы сможете на сайте «Математика для школьников» (http://www.kenqyry.com/).
На сайте http://www.kaser.com/ вы сможете скачать демонстрационную версию очень полезной, развивающей логику и умение рассуждать логической головоломки Шерлок.
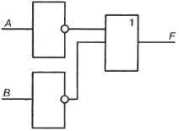
1.3.6. Логические элементы
Алгебра логики — раздел математики, играющий важную роль в конструировании автоматических устройств, разработке аппаратных и программных средств информационных и коммуникационных технологий.
Вы уже знаете, что любая информация может быть представлена в дискретной форме — в виде фиксированного набора отдельных значений. Устройства, которые обрабатывают такие значения (сигналы), называются дискретными. Дискретный преобразователь, который выдаёт после обработки двоичных сигналов значение одной из логических операций, называется логическим элементом.
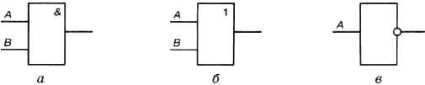
На рис. 1.5 приведены условные обозначения (схемы) логических элементов, реализующих логическое умножение, логическое сложение и инверсию.
Рис 1.5.
Логические элементы
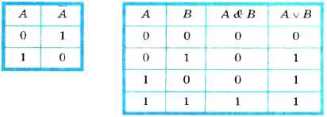
Логический элемент И (конъюнктор) реализует операцию логического умножения (рис. 1.5, а). Единица на выходе этого элемента появится только тогда, когда на всех входах будут единицы.
Логический элемент ИЛИ (дизъюнктор) реализует операцию логического сложения (рис. 1.5, б). Если хотя бы на одном входе будет единица, то на выходе элемента также будет единица.
Логический элемент НЕ (инвертор) реализует операцию отрицания (рис. 1.5, в). Если на входе элемента О, то на выходе 1 и наоборот.
Компьютерные устройства, производящие операции над двоичными числами, и ячейки, хранящие данные, представляют собой электронные схемы, состоящие из отдельных логических элементов. Более подробно эти вопросы будут раскрыты в курсе информатики 10-11 классов.
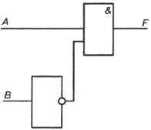
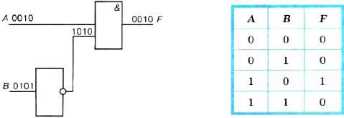
Пример 3. Проанализируем электронную схему, т. е. выясним, какой сигнал должен быть на выходе при каждом возможном наборе сигналов на входах.
Решение. Все возможные комбинации сигналов на входах А к В внесём в таблицу истинности. Проследим преобразование каждой пары сигналов при прохождении их через логические элементы и запишем полученный результат в таблицу. Заполненная таблица истинности полностью описывает рассматриваемую электронную схему.
Таблицу истинности можно построить и по логическому выражению, соответствующему электронной схеме. Последний логический элемент в рассматриваемой схеме — конъюнктор. В него поступают сигналы от входа Л и от инвертора. В свою очередь, в инвертор поступает сигнал от входа В. Таким образом,
Составить более полное представление о логических элементах и электронных схемах вам поможет работа с тренажёром «Логика» (http://kpolyakov. narod. ru/prog/logic. htm).
Самое главное
Высказывание — это предложение на любом языке, содержание которого можно однозначно определить как истинное или ложное.
Основные логические операции, определённые над высказываниями: инверсия, конъюнкция, дизъюнкция.
Таблицы истинности для основных логических операций:
При вычислении логических выражений сначала выполняются действия в скобках. Приоритет выполнения логических операций:
Вопросы и задания
На них изображены известные вам из курса физики параллельное и последовательное соединения переключателей. В первом случае, чтобы лампочка загорелась, должны быть включены оба переключателя. Во втором случае достаточно, чтобы был включён один из переключателей. Попытайтесь самостоятельно провести аналогию между элементами электрических схем и объектами и операциями алгебры логики:
По запросу сомики & гуппи было найдено 0 сайтов, по запросу сомики & меченосцы — 20 сайтов, а по запросу меченосцы & гуппи — 10 сайтов.
Сколько сайтов будет найдено по запросу сомики | меченосцы | гуппи?
Для скольких сайтов рассматриваемого сегмента ложно высказывание «Сомики — ключевое слово сайта ИЛИ меченосцы — ключевое слово сайта ИЛИ гуппи — ключевое слово сайта»?
Смит: «Я не делал этого. Браун сделал это».
Джон: «Браун не виновен. Смит сделал это».
Браун: «Я не делал этого. Джон не делал этого».
Суд установил, что один из них дважды солгал, другой дважды сказал правду, третий один раз солгал, один раз сказал правду. Кто из подозреваемых должен быть оправдан?
Электронное приложение к уроку
Ссылки на ресурсы ЕК ЦОР
Федеральный центр информационных образовательных ресурсов:
Свободное программное обеспечение:
 |  |  |
| Презентации, плакаты, текстовые файлы | Вернуться к материалам урока | Ресурсы ЭОР |
Cкачать материалы урока
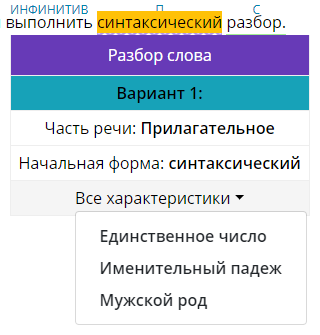
Синтаксический разбор предложения в тексте
Чтобы сделать синтаксический разбор предложений в тексте, введите текст в текстовое поле и нажмите кнопку разобрать.
Как программа делает разбор предложений?
Программа разбивает весь текст по словам и предложениям, далее разбирает каждое слово по отдельности, выделяет морфологические признаки и начальную форму слова.
Оцените нашу программу ниже, оставляйте комментарии, мы обязательно ответим.
Характеристика предложения
| По цели высказывания |
|---|
| По интонации (по эмоциональной окраске) |
| По количеству грамматических основ |
| По количеству главных членов предложения |
| По наличию второстепенных членов |
| — |
О инструменте
После того как вы нажмете кнопку «Разобрать», вы получите результат синтаксического разбора предложения. Сверху результата будет указано количество символов в тексте и количество слов.
Каждая часть речи подсвечивается отдельным цветом, если вы хотите отображать только определенные части речи в предложении, выберите в панели инструментов нужную вам часть.
Какой вариант разбора выбрать?
Омонимы — это слова одинаковые по написанию, но разные по значению, такие слова могут попасться в предложении и программа не может определить какой смысл несет слово. Здесь нужно выбрать подходящей разбор слова в предложение, смотрите по контексту.
Для этого вам помогут морфологические признаки слова, чтобы их увидеть наведите на слово и в раскрывающемся меню выберите «Все характеристики».
Часть речи сверху слова
Чтобы показывать часть речи сверху слова, включите соответствующею функцию в настройке разбора.